
【题目】如图,已知反比例函数![]() 与一次函数
与一次函数![]() 的图象交于点A(1,8)、B(-4,m).
的图象交于点A(1,8)、B(-4,m).
(1)求k1、k2、b的值;
(2)求△AOB的面积;
(3)请直接写出不等式![]() 的解集;
的解集;
(4)若M(x1,y1)、N(x2,y2)是反比例函数![]() 图象上的两点,且x1<x2,y1<y2,指出点M、N各位于哪个象限,并说明理由.
图象上的两点,且x1<x2,y1<y2,指出点M、N各位于哪个象限,并说明理由.
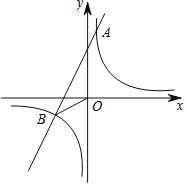
【答案】(1)k1=8,k2=2,b=6;(2)15;(3)-4<x<0或x>1;(4)M(x1,y1)在第三象限,N(x2,y2)在第一象限.
【解析】试题分析:
(1)先把点A、B的坐标代入反比例函数的解析式求得k1和m的值,从而可得反比例函数的解析式和点B的纵坐标;再把点A、B的坐标代入![]() 列方程组可解得k2和b;
列方程组可解得k2和b;
(2)如图,连接OA,由(1)中所求一次函数的解析式求得直线AB与y轴的交点坐标C的坐标,由S△AOB=S△BOC+S△AOC即可求出所求面积;
(3)观察图象找到一次函数图象在反比例函数图象之上部分所对应的自变量的取值范围即可;
(4)因为在反比例函数中,k1=8>0,所以在每个象限内,反比例函数值y都随x的增大而减小,所以点M、N位于不同的分支上,结合x1<x2,y1<y2即可得到答案.
试题解析:
(1)∵反比例函数y=![]() 与一次函数y=k2x+b的图象交于点A(1,8)、B(-4,m),
与一次函数y=k2x+b的图象交于点A(1,8)、B(-4,m),
∴k1=1×8=8,m=8÷(-4)=-2,
∴点B的坐标为(-4,-2).
将A(1,8)、B(-4,-2)代入y2=k2x+b中,
![]() ,解得:
,解得: ![]() .
.
∴k1=8,k2=2,b=6;
(2)如图,连接OA,设直线AB和y轴相交于点C,
∵当x=0时,y2=2x+6=6,
∴直线AB与y轴的交点C的坐标为(0,6).
∴S△AOB=S△BOC+S△AOC![]() ×6×4+
×6×4+![]() ×6×1=15;
×6×1=15;
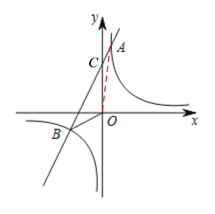
(3)观察函数图象可知:当-4<x<0或x>1时,一次函数的图象在反比例函数图象的上方,
∴不等式![]() <k2x+b的解为:-4<x<0或x>1;
<k2x+b的解为:-4<x<0或x>1;
(4)∵比例函数y=![]() 的图象位于第一、三象限,
的图象位于第一、三象限,
∴在每个象限内,y随x的增大而减小,
∵x1<x2,y1<y2,
∴M,N在不同的象限,
∴M(x1,y1)在第三象限,N(x2,y2)在第一象限.


 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案科目:初中数学 来源: 题型:
【题目】某校利用暑假进行田径场的改造维修,项目承包单位派遣一号施工队进场施工,计划用50天时间完成整个工程:当一号施工队工作5天后,承包单位接到通知,有一大型活动要在该田径场举行,要求比原计划提前18天完成整个工程,于是承包单位派遣二号与一号施工队共同完成剩余工程,结果按通知要求如期完成整个工程.
(1)若二号施工队单独施工,完成整个工程需要多少天?
(2)若此项工程一号、二号施工队同时进场施工,完成整个工程需要多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,∠B的角平分线BE与AD交于点E,∠BED的角平分线EF与DC交于点F,若AB=9,DF=2FC,则BC= .(结果保留根号)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A(-4,![]() )、B(2,-4)是一次函数
)、B(2,-4)是一次函数![]() 的图象和反比例函数
的图象和反比例函数![]() 的图象的两个交点.
的图象的两个交点.
(1)求反比例函数和一次函数的解析式;
(2)求直线AB和![]() 轴的交点C的坐标;
轴的交点C的坐标;
(3)求方程![]() 的解(请直接写出答案);
的解(请直接写出答案);
(4)求不等式![]() 的解集(请直接写出答案).
的解集(请直接写出答案).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△AOB是等边三角形,且B(2,0),OC是AB边的中线,将△AOB绕点O逆时针旋转120°得到△A1OB1.
(1)B1的坐标是_______(直接写出结果即可);
(2)请画出将△A1OB1绕点O逆时针旋转120°得到的△A2OB2,并按图形旋转规律画出阴影部分;
(3)计算点B旋转到点B1所经过的弧形路线长(结果保留π).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为迎接中国森博会,某商家计划从厂家采购A,B两种产品共20件,产品的采购单价(元/件)是采购数量(件)的一次函数,下表提供了部分采购数据.
采购数量(件) | 1 | 2 | … |
A产品单价(元/件) | 1480 | 1460 | … |
B产品单价(元/件) | 1290 | 1280 | … |
(1)设A产品的采购数量为x(件),采购单价为y1(元/件),求y1与x的关系式;
(2)经商家与厂家协商,采购A产品的数量不少于B产品数量的![]() ,且A产品采购单价不低于1200元,求该商家共有几种进货方案;
,且A产品采购单价不低于1200元,求该商家共有几种进货方案;
(3)该商家分别以1760元/件和1700元/件的销售单价售出A,B两种产品,且全部售完,在(2)的条件下,求采购A种产品多少件时总利润最大,并求最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店需要购进甲、乙两种商品共160件,其进价和售价如下表:(注:获利=售价-进价)

(1)若商店计划销售完这批商品后能获利1100元,问甲、乙两种商品应分别购进多少件?
(2)若商店计划投入资金少于4300元,且销售完这批商品后获利多于1260元,请问有哪几种购货方案?并直接写出其中获利最大的购货方案。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一只不透明的袋子中装有4个大小、质地都相同的乒乓球,球面上分别标有数字1、2、3、4.
(1)搅匀后从中任意摸出1个球,求摸出的乒乓球球面上数字为1的概率;
(2)搅匀后先从中任意摸出1个球(不放回),再从余下的3个球中任意摸出1个球,求2次摸出的乒乓球球面上数字之和为偶数的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com