
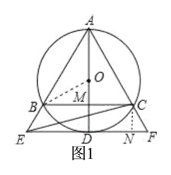
【题目】如图,⊙O是△ABC的外接圆,AD是⊙O的直径,AD与BC相交于点M,且BM=MC,过点D作BC的平行线,分别与AB、AC的延长线相交于点E、F.
(1)求证:EF与⊙O相切;
(2)若BC=2![]() ,MD=
,MD=![]() ,求CE的长.
,求CE的长.

【答案】(1)见解析;(2)![]()
【解析】试题分析:
(1)由AD是⊙O的直径,BM=MC可得AD⊥BC,结合EF∥BC可得AD⊥EF,从而根据“切线的判定定理”可得EF与⊙O相切;
(2)如图1,连接OB,过点C作CN⊥EF于点N.先证△OBM是Rt△,由勾股定理建立方程解此OB的长,因此可得AD的长和AM的长;证△ABC∽△AEF,从而可解得EF的长;在Rt△AMC中,计算出tan∠AMC的值,从而可得∠MAC=30°,由此可得∠NCF=30°,结合CN=MD可在Rt△NCF中解得得NF的长,即可由EN=EF-NF得到EN的长,这样在Rt△ECN中即可由勾股定理解得CE的长了.
试题解析:
(1)∵AD是⊙O的直径,AD与BC相交于点M,且BM=MC,
∴AD⊥BC,
∵EF∥BC,
∴AD⊥EF,
∴EF与⊙O相切;
(2)连接OB,
在△OBM中,BM2+OM2=OB,即(![]() )+(OB﹣
)+(OB﹣![]() )=OB2,OB=2
)=OB2,OB=2![]()
∴OM=MD=![]() ,
,
∵BC∥EF,
∴△ABC∽△AEF
∴![]() ,
,
∴EF=![]() =
=![]() =
=![]() ,
,
∵tan∠CAM=![]() ,
,
∴∠CAM=30°,
作CN⊥EF,
∵AD⊥EF,
∴CN∥AD,
∴∠FCN=∠CAM=30°,
∵BC∥EF,
∴四边形MDNC是矩形,
∴CN=MD=![]() ,
,
∴NF=CNtan30°=![]() ×
×![]() =
=![]() ,
,
∴EN=EF﹣NF=![]() ﹣
﹣![]() =
=![]() ,
,
∴EC=![]() =
=![]() .
.


 天天练口算系列答案
天天练口算系列答案科目:初中数学 来源: 题型:
【题目】某地为提倡节约用水,准备实行自来水“阶梯计费”方式,用户用水不超出基本用水量的部分享受基本价格,超出基本用水量的部分实行加价收费,为更好地决策,自来水公司随机抽取部分用户的用适量数据,并绘制了如下不完整统计图(每组数据包括右端点但不包括左端点),请你根据统计图解决下列问题:

(1)此次调查抽取了多少用户的用水量数据?
(2)补全频数分布直方图,求扇形统计图中“25吨~30吨”部分的圆心角度数;
(3)如果自来水公司将基本用水量定为每户25吨,那么该地20万用户中约有多少用户的用水全部享受基本价格?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分8分)如图,在△ABC中,AB=AC,∠DAC是△ABC的一个外角.
实践与操作:
根据要求尺规作图,并在图中标明相应字母(保留作图痕迹,不写作法).

(1)作∠DAC的平分线AM;
(2)作线段AC的垂直平分线,与AM交于点F,与BC边交于点E,连接AE、CF.
猜想并证明:
判断四边形AECF的形状并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,∠E=∠F=90°,∠B=∠C,AE=AF.有以下结论:①EM=FN;②CD=DN;③∠FAN=∠EAM;④△ACN≌△ABM.其中正确的有( ).

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】父亲两次将100斤粮食分给兄弟俩,第一次分给哥哥的粮食等于第二次分给弟弟的2倍,第二次分给哥哥的粮食是第一次分给弟弟的3倍,求两次分粮食中,哥哥、弟弟各分到多少粮食?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本小题满分13分)
某公司经销农产品业务,以3万元/吨的价格向农户收购农产品后,以甲、乙两种方式进行销售,甲方式包装后直接销售;乙方式深加工后再销售.甲方式农产品的包装成本为1万元/吨,根据市场调查,它每吨平均销售价格y(单位:万元)与销售量m(单位:吨)之间的函数关系为y = -m+14(2≤m≤8);乙方式农产品深加工等(不含进价)总费用S(单位:万元)与销售量n(单位:吨)之间的函数关系是S=3n+12,平均销售价格为9万元/吨.
参考公式:抛物线y=ax2+bx+c(a≠0)的顶点坐标是(-![]() ,
,![]() )
)
(1)该公司收购了20吨农产品,其中甲方式销售农产品x吨,其余农产品用乙方式销售,经销这20吨农产品所获得的毛利润为w万元(毛利润=销售总收入-经营总成本).
①直接写出:甲方式购买和包装x吨农产品所需资金为_________万元;乙方式购买和加工其余农产品所需资金为_________万元;
②求出w关于x的函数关系式;
③若农产品全部销售该公司共获得了48万元毛利润,求x的值;
④若农产品全部售出,该公司的最小利润是多少.
(2)该公司现有流动资金132万元,若将现有流动资金全部用于经销农产品,
①其中甲方式经销农产品x吨,则总经销量p为__________吨(用含x的代数式表示);
②当x为何值时,使公司获得最大毛利润,并求出最大毛利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是菱形,∠A=60°,AB=2,扇形BEF的半径为2,圆心角为60°,则图中阴影部分的面积是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某次大型活动,组委会启用无人机航拍活动过程,在操控无人机时应根据现场状况调节高度,已知无人机在上升和下降过程中速度相同,设无人机的飞行高度h(米)与操控无人机的时间t(分钟)之间的关系如图中的实线所示,根据图象回答下列问题:
(1)图中的自变量是______,因变量是______;
(2)无人机在75米高的上空停留的时间是______分钟;
(3)在上升或下降过程中,无人机的速度______为米/分;
(4)图中a表示的数是______;b表示的数是______;
(5)图中点A表示______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在离水面高度为5m的岸上有人用绳子拉船靠岸,开始绳子与水面的夹角为30°,此人以每秒0.5m的速度收绳.
(1)8秒后船向岸边移动了多少米?
(2)写出还没收的绳子的长度S米与收绳时间t秒的函数关系式.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com