
【题目】如图,已知正方形ABCD,将一块等腰直角三角板的锐角顶点与A重合,并将三角板绕A点旋转,如图1,使它的斜边与BD交于点H,一条直角边与CD交于点G.
(1)请适当添加辅助线,通过三角形相似,求出![]() 的值;
的值;
(2)连接GH,判断GH与AF的位置关系,并证明;
(3)如图2,将三角板旋转至点F恰好在DC的延长线上时,若AD=![]() ,AF=
,AF=![]() .求DG的长.
.求DG的长.

【答案】(1)![]() ;(2)GH⊥AF,理由见解析;(3)
;(2)GH⊥AF,理由见解析;(3)![]()
【解析】试题分析:(1)连接AC,利用等量代换,求出∠BAH=∠GAC,再加上45的角,即可求出△BAH∽△CAG,进而得出结论;(2)先回答位置关系GH⊥AF,再证明,利用(1)问的结论,利用两边对应成比例且夹角相等得出△HAG∽△EAF,得出比例式即可;(3)判断出△AGD∽△FGE,得出![]() ,设出未知数,求出AG、EG的长度,利用相似即可求出DG的长度.
,设出未知数,求出AG、EG的长度,利用相似即可求出DG的长度.
试题解析:
(1)连接AC
∵四边形ABCD是正方形
∴∠BAC=∠ABH=∠ABH=45, ![]()
又∵△AEF是等腰直角三角形
∴∠EAH=45
∴∠BAH+∠EAC=∠FAC+∠EAC=45
∴∠BAH=∠GAC
∴△BAH∽△CAG.
∴![]()
(2)GH⊥AF,理由如下:
∵在Rt△AEF中, ![]()
∴![]()
又∵∠HAG=∠EAF
∴△HAG∽△EAF.
∴∠AHG=∠E=90
∴GH⊥AF..
(3)∵在Rt△AGH中, ![]()
∴AG=![]() GH
GH
又∵∠ADG=∠E=90,∠AGD=∠FGE
∴△AGD∽△FGE
∴![]() .
.
又∵在Rt△AEF中,AF=![]()
∴EF=5
∴![]()
∴![]()
∴![]()
∴可设GH为![]() ,则
,则![]()
∴AF=AH+FH=![]()
∴![]()
∴AG=![]() GH
GH![]()
∴![]()
又∵![]()
∴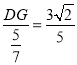
∴DG=![]()


科目:初中数学 来源: 题型:
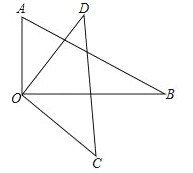
【题目】如图,将一副三角板中的两块直角三角尺的直角顶点O按如图方式叠放在一起.
(1)若∠BOD=35°,则∠AOC= ;
(2)若∠AOC=135°,则∠BOD= ;
(3)猜想∠AOC与∠BOD的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有下列四个命题:
①经过三个点一定可以作圆;
②等弧所对的圆周角相等;
③三角形的外心到三角形各顶点的距离都相等;
④在同圆中,平分弦的直径一定垂直于这条弦.
其中正确的有()
A.0B.1C.2D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知x=3,求6x2+4x﹣2(x2﹣1)﹣2(2x+x2)的值,小民粗心把x=3抄成了x=﹣3,但计算的结果却正确的.你知道其中的原因吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知M(a,b)是平面直角坐标系xOy中的点,其中a是从l,2,3,4三个数中任取的一个数,b是从l,2,3,4,5五个数中任取的一个数.定义“点M(a,b)在直线x+y=n上”为事件Qn(2≤n≤9,n为整数),则当Qn的概率最大时,n的所有可能的值为( )
A.5
B.4或5
C.5或6
D.6或7
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com