已知一元二次方程x2+px+q+1=0的一根为2.
(1)求q关于p的关系式;
(2)求证:抛物线y=x2+px+q与x轴有两个交点;
(3)设抛物线y=x2+px+q的顶点为M,且与x轴相交于A(x1,0)、B(x2,0)两点,求使△AMB面积最小时的抛物线的解析式.
【答案】
分析:(1)把x=2代入可求得q与p的关系式;
(2)由△=b
2-4ac可判断抛物线与x轴的交点情况;
(3)先写出该抛物线的顶点坐标,方程根与系数关系可求线段AB的长,进而求得△AMB的面积表达,从而求得最小值.
解答:(1)解:把x=2代入得2
2+2p+q+1=0,即q=-(2p+5);
(2)证明:∵一元二次方程x
2+px+q=0的判别式△=p
2-4q>0,
由(1)得△=p
2+4(2p+5)=p
2+8p+20=(p+4)
2+4>0,(3分)
∴一元二次方程x
2+px+q=0有两个不相等的实根.(4分)
∴抛物线y=x
2+px+q与x轴有两个交点;(5分)
(3)解:抛物线顶点的坐标为
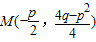
,(6分)
∵x
1,x
2是方程x
2+px+q=0的两个根,
∴
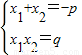
,
∴

.(7分)
∴
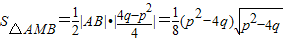
,(8分)
要使S
△AMB最小,只须使p
2-4q最小.
由(2)得△=p
2-4q=(p+4)
2+4,
所以当p=-4时,有最小值4,此时S
△AMB=1,q=3.(9分)
故抛物线的解析式为y=x
2-4x+3.(10分)
点评:考查了代入法、判别式△的使用,以及一元二次方程中根与系数的关系、三角形面积的求法、最大最小值的求解等内容.

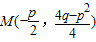 ,(6分)
,(6分)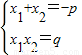 ,
, .(7分)
.(7分)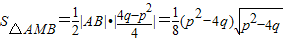 ,(8分)
,(8分)

 优加精卷系列答案
优加精卷系列答案