
【题目】在一次800米的长跑比赛中,甲、乙两人所跑的路程![]() (米)与各自所用时间
(米)与各自所用时间![]() (秒)之间的函数图象分别为线段
(秒)之间的函数图象分别为线段![]() 和折线
和折线![]() (如图所示),请根据图象,回答下列问题.
(如图所示),请根据图象,回答下列问题.
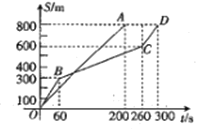
(1)在起跑后60秒时,乙在甲的前面还是后面?
(2)在起跑后多少秒时,两人相遇?
科目:初中数学 来源: 题型:
【题目】如图,在RT△ABC中,∠ACB=90°,∠B=35°,CD⊥AB,垂足为点D,

(1)求∠ACD的度数;
(2)找出图中相等的角,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,任意一个有理数与无理数的和为无理数,任意一个不为零的有理数与一个无理数的积为无理数,而零与无理数的积为零.由此可得:如果mx+n=0,其中m、n为有理数,x为无理数,那么m=0且n=0.
(1)如果![]() ,其中a、b为有理数,那么a= ,b= .
,其中a、b为有理数,那么a= ,b= .
(2)如果![]() ,其中a、b为有理数,求a+2b的值.
,其中a、b为有理数,求a+2b的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店欲购进一批跳绳,若购进![]() 种跳绳
种跳绳![]() 根和
根和![]() 种跳绳
种跳绳![]() 根,则共需
根,则共需![]() 元;若购进
元;若购进![]() 种跳绳
种跳绳![]() 根和
根和![]() 种跳绳
种跳绳![]() 根,则共需
根,则共需![]() 元.
元.
(1)求![]() 、
、![]() 两种跳绳的单价各是多少?
两种跳绳的单价各是多少?
(2)若该商店准备购进这两种跳绳共![]() 根,且
根,且![]() 种跳绳的数量不少于跳绳总数量的
种跳绳的数量不少于跳绳总数量的![]() .若每根
.若每根![]() 种、
种、![]() 种跳绳的售价分别为
种跳绳的售价分别为![]() 元、
元、![]() 元,问:该商店应如何进货才可获取最大利润,并求出最大利润.
元,问:该商店应如何进货才可获取最大利润,并求出最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)①如图①![]() 的内角
的内角![]() 的平分线与内角
的平分线与内角![]() 的平分线相交于
的平分线相交于![]() 点,请探究
点,请探究![]() 与
与![]() 的关系,并说明理由.
的关系,并说明理由.
②如图②,![]() 的内角
的内角![]() 的平分线与外角
的平分线与外角![]() 的平分线相交于
的平分线相交于![]() 点,请探究
点,请探究![]() 与
与![]() 的关系,并说明理由.
的关系,并说明理由.
(2)如图③④,四边形![]() 中,设
中,设![]() ,
,![]() ,
,![]() 为四边形
为四边形![]() 的内角
的内角![]() 与外角
与外角![]() 的平分线所在直线相交而行成的锐角.请利用(1)中的结论完成下列问题:
的平分线所在直线相交而行成的锐角.请利用(1)中的结论完成下列问题:
①如图③,求![]() 的度数.(用
的度数.(用 ![]() 的代数式表示)
的代数式表示)
②如图④,将四边形![]() 沿着直线
沿着直线![]() 翻折得到四边形
翻折得到四边形![]() ,
,![]() 为
为![]() 延长线上一点,连接
延长线上一点,连接![]() ,
,![]() 与
与![]() 的角平分线交于点
的角平分线交于点![]() ,求
,求![]() 与
与![]() 的数量关系.
的数量关系.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】昆明某家电专卖店销售每台进价分别200元、160元的A,B两种型号的电风扇,下表是近两周的销售情况

(注:进价、售价均保持不变,利销=销售收入进货成本)
(1)求A,B两种型号的电风扇的销售单价;
(2)若专卖店准备用不多于3560元的金额再采购这两种型号的电风扇共20台,且采购A型电风扇的数量不少于8台.求专卖店有哪几种采购方案?
(3)在(2)的条件下.如果采购的电风扇都能销售完,请直接写出哪种采购方案专卖店所获利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AB=4cm,∠BAD=60°.动点E、F分别从点B、D同时出发,以1cm/s的速度向点A、C运动,连接AF、CE,取AF、CE的中点G、H,连接GE、FH.设运动的时间为ts(0<t<4).
(1)求证:AF∥CE;
(2)当t为何值时,四边形EHFG为菱形;
(3)试探究:是否存在某个时刻t,使四边形EHFG为矩形,若存在,求出t的值,若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1,线段AB、CD相交于点O,连接AD、CB,我们把形如图1的图形称之为“8字形”.如图2,在图1的条件下,∠DAB和∠BCD的平分线AP和CP相交于点P,并且与CD、AB分别相交于M、N.试解答下列问题:
(1)在图1中,请直接写出∠A、∠B、∠C、∠D之间的数量关系: ;
(2)仔细观察,在图2中“8字形”的个数: 个;
(3)图2中,当∠D=50度,∠B=40度时,求∠P的度数.
(4)图2中∠D和∠B为任意角时,其他条件不变,试问∠P与∠D、∠B之间存在着怎样的数量关系.(直接写出结果,不必证明).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com