证明:因为x0,y0是方程①的整数解,当然满足ax0+by0=c,②
因此a(x0-bt)+b(y0+at)=ax0+by0=c.
这表明x=x0-bt,y=y0+at也是方程①的解.
设x′,y′是方程①的任一整数解,则有
ax′+by′=c.③
③-②得
a(x′-x0)=b′(y0-y′).④
∵a,b是互质的正整数即(a,b)=1,
∴即y′=y0+at,其中t是整数.将y′=y0+at代入④,即得x′=x0-bt.
∴x′,y′可以表示成x=x0-bt,y=y0+at的形式,
∴x=x0-bt,y=y0+at表示方程①的一切整数解.
分析:把x0,y0代入原方程中可得到一个方程,设方程的任一组解可得到第二个方程,联立两个方程求解,再根据a,b是互质的正整数,c是整数,即可得到原方程解的表示形式,即可证明结论.
点评:本题考查了二元一次方程的解和二元一次方程组的解.当没有条件限制时,二元一次方程的解有无数个.求不定方程的整数解,先将方程做适当变形,确定其中一个未知数的取值范围,然后列举出适合条件的所有整数值,再求出另一个未知数的值.

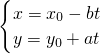 ,其中t=0,±1,±2,±3,….
,其中t=0,±1,±2,±3,….

 阅读快车系列答案
阅读快车系列答案