
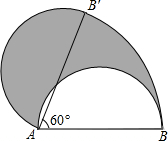
 如图,直径AB为6的半圆,绕点A逆时针旋转60°此时点B到达点B′,求圆中阴影部分的面积.
如图,直径AB为6的半圆,绕点A逆时针旋转60°此时点B到达点B′,求圆中阴影部分的面积. 分析 根据题意得出AB=AB′=6,∠BAB′=60°,根据图形得出图中阴影部分的面积S=$\frac{60π×(6÷2)^{2}}{360}$+$\frac{1}{2}$π×(6÷2)2-$\frac{1}{2}$π×(6÷2)2,求出即可.
解答 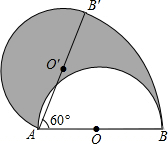 解:∵AB=AB′=6,∠BAB′=60°
解:∵AB=AB′=6,∠BAB′=60°
∴图中阴影部分的面积是:
S=S扇形B′AB+S半圆O′-S半圆O
=$\frac{60π×(6÷2)^{2}}{360}$+$\frac{1}{2}$π×(6÷2)2-$\frac{1}{2}$π×(6÷2)2
=1.5π.
答:圆中阴影部分的面积是1.5π.
点评 本题考查了旋转的性质,扇形的面积的应用,通过做此题培养了学生的计算能力和观察图形的能力,题目比较好,难度适中.


科目:初中数学 来源: 题型:选择题
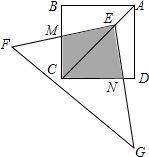 如图,点E在正方形ABCD对角线AC上,且EC=2AE,Rt△FEG的两直角边EF、EG分别交BC、DC于点M、N.若正方形的边长为a,则重叠部分的面积为( )
如图,点E在正方形ABCD对角线AC上,且EC=2AE,Rt△FEG的两直角边EF、EG分别交BC、DC于点M、N.若正方形的边长为a,则重叠部分的面积为( )| A. | $\frac{5}{9}$a2 | B. | $\frac{4}{9}$a2 | C. | $\frac{2}{3}$a2 | D. | $\frac{1}{4}$a2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
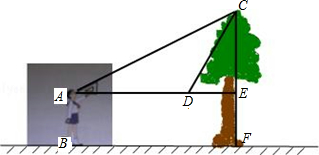 如图,小敏同学想测量一棵大树的高度.她站在B处仰望树顶,测得仰角为30°,再往大树的方向前进4m,测得仰角为60°,已知小敏同学身高AB为1.7m,求这棵树的高度.(结果精确到0.1m,$\sqrt{3}$≈1.73)
如图,小敏同学想测量一棵大树的高度.她站在B处仰望树顶,测得仰角为30°,再往大树的方向前进4m,测得仰角为60°,已知小敏同学身高AB为1.7m,求这棵树的高度.(结果精确到0.1m,$\sqrt{3}$≈1.73)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系.根据图象进行以下探究:
一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系.根据图象进行以下探究:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| a | b | c | a+b-c | $\frac{s}{l}$ |
| 3 | 4 | 5 | 2 | $\frac{1}{2}$ |
| 5 | 12 | 13 | 4 | 1 |
| 8 | 15 | 17 | 6 | $\frac{3}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,平面上有A、B、C三点.
如图,平面上有A、B、C三点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a8-b8 | B. | a8-2a4b4+b8 | C. | a8+b8 | D. | a8+2a4b4+b8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com