

���� ��1����B���������y=$\frac{k}{x}$�����k��ֵ��
��2���ֱ��B��D��x��Ĵ��ߣ�����ֱ�ΪE��F����֤�á�ABE�ա�DAF�������DF=AE��AF=BE�������OF=OD���ٴ���y=-$\frac{4}{x}$�����D�����꣬������OA�ij��������A�����ꣻ
��3���ɹ��ɶ��������BD�ij�����֪AC�ij���������C�����꣬�����BC���е����꣬���ı���MCNBΪƽ���ı��ο�֪MN��BC��MN����ƽ�֣���M������Ϊ��x��0������ɱ�ʾ��N�����꣬����y=$\frac{k}{x}$�����x��ֵ��������M��N�����꣮
��� �⣺
��1���ߵ�B��3��3����˫����y=$\frac{k}{x}$��x��0���ϣ�
��3=$\frac{k}{3}$��
��k=9��
��2���ֱ��B��D��x��Ĵ��ߣ�����ֱ�ΪE��F��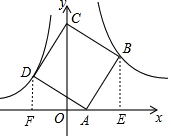
���ı���ABCDΪ�����Σ�
��AB=AD����DAB=90�㣬
���FDA+��DAF=��DAF+��BAE=90�㣬
���FDA=��BAE��
�ڡ�ABE�͡�DAF��
$\left\{\begin{array}{l}{��BAE=��FDA}\\{��BEA=��DFA}\\{AB=AD}\end{array}\right.$
���ABE�ա�DAF��AAS����
��AF=BE��DF=AE��
��B��3��3����
��BE=OE=AF=3��
��FO=AE=DF��
�����D��������x��-x����x��0����
�ߵ�D��˫����y=-$\frac{4}{x}$��x��0���ϣ�
��-x2=-4�����x=2����ȥ����x=-2��
��D��-2��2����
��OF=2��
��OA=AF-OF=3-2=1��
��A��1��0����
��3����B��3��3����D��-2��2����
��BD=$\sqrt{[3-��-2��]^{2}+��3-2��^{2}}$=$\sqrt{26}$��
���ı���ABCDΪ�����Σ�
��AC=BD=$\sqrt{26}$��
��OA2+OC2=26����12+OC2=26�����OC=5��
��C��0��5����
��BC���е�ΪH����H��$\frac{3}{2}$��4����
���ı���MCNBΪƽ���ı��Σ�
��MN���е�ҲΪH��
��M��x���ϣ�
�����M��t��0����N��m��n����
��t+m=2��$\frac{3}{2}$=3��n=8��
��N��3-t��8����
�ߵ�N�ڷ���������y=$\frac{9}{x}$��x��0���ϣ�
��8��3-t��=9�����t=$\frac{15}{8}$��
��M��$\frac{15}{8}$��0����N��$\frac{9}{8}$��8��������������������M��N��
���� ����Ϊ�������������ۺ�Ӧ�ã��漰����ϵ������ȫ�������ε��ж������ʡ������ε����ʡ����ɶ�����ƽ���ı��ε����ʡ�����˼���֪ʶ���ڣ�1����ע�⺯��ͼ���ϵĵ���������㺯������ʽ���ڣ�2����֤��OF=AE�ǽ���Ĺؼ��������D�����꣬�ڣ�3����ע��BC���е�Ҳ���߶�MN���е��ǽ���Ĺؼ������⿼��֪ʶ��϶࣬�ۺ��Խ�ǿ���Ѷ����У�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
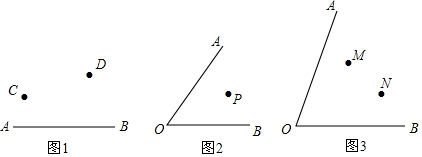
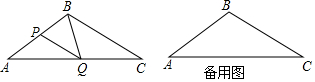
 ��Ҫ����ͼ ��ͼ����ͬһƽ�������ĸ���A��B��C��D
��Ҫ����ͼ ��ͼ����ͬһƽ�������ĸ���A��B��C��D�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ���� | B�� | ���� | C�� | 0 | D�� | ��ȷ�� |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com