
分析 (1)由销售单价每涨1元,就会少售出10件玩具得y=600-(x-40)×10=1000-10x,利润W=(1000-10x)(x-30)=-10x2+1300x-30000;
(2)令-10x2+1300x-30000=10000,求出x的值即可;
(3)首先求出x的取值范围,然后把w=-10x2+1300x-30000转化成y=-10(x-65)2+12250,结合x的取值范围,求出最大利润.
解答 解:(1)y=600-(x-40)×10=1000-10x,
W=(1000-10x)(x-30)=-10x2+1300x-30000;
(2)-10x2+1300x-30000=10000
解之得:x1=50,x2=80
答:玩具销售单价为50元或80元时,可获得10000元销售利润,
(3)根据题意得
$\left\{\begin{array}{l}{1000-10x≥540}\\{x≥44}\end{array}\right.$,
解之得:44≤x≤46,
w=-10x2+1300x-30000=-10(x-65)2+12250,
∵a=-10<0,对称轴是直线x=65,
∴当44≤x≤46时,w随x增大而增大.
∴当x=46时,W最大值=8640(元).
答:商场销售该品牌玩具获得的最大利润为8640元.
点评 本题主要考查了二次函数的应用的知识点,解答本题的关键熟练掌握二次函数的性质以及二次函数最大值的求解,此题难度不大.


科目:初中数学 来源: 题型:解答题
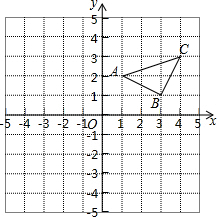 作图题(不写作法)已知:如图,在平面直角坐标系中.
作图题(不写作法)已知:如图,在平面直角坐标系中.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
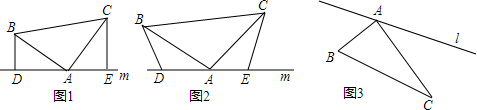
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
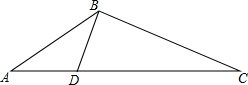 在△ABC中,D是边BC上一点,且∠ABD=∠C.
在△ABC中,D是边BC上一点,且∠ABD=∠C.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 相似三角形周长之比等于对应高之比 | |
| B. | 两个等腰直角三角形一定相似 | |
| C. | 各有一个角等于91°的两个等腰三角形相似 | |
| D. | 两边对应成比例且有一个角相等的两个三角形相似 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com