
分析 (1)利用分母有理化的方法解答;
(2)根据平方差公式计算即可;
(3)利用阅读材料的结论和二次根式的加减混合运算法则计算.
解答 解:(1)$\frac{1}{\sqrt{n+1}+\sqrt{n}}$=$\frac{\sqrt{n+1}-\sqrt{n}}{(\sqrt{n+1}+\sqrt{n})(\sqrt{n+1}-\sqrt{n})}$=$\sqrt{n+1}$-$\sqrt{n}$,
故答案为:$\sqrt{n+1}$-$\sqrt{n}$;
(2)($\sqrt{n+1}+\sqrt{n}$)($\sqrt{n+1}-\sqrt{n}$)=($\sqrt{n+1}$)2-($\sqrt{n}$)2=1,
故答案为:1;
(3)($\frac{1}{\sqrt{2}+1}$+$\frac{1}{\sqrt{3}+\sqrt{2}}$+$\frac{1}{\sqrt{4}+\sqrt{3}}$+…+$\frac{1}{\sqrt{2017}+\sqrt{2016}}$)($\sqrt{2017}+1$)
=($\sqrt{2}$-1+$\sqrt{3}$-$\sqrt{2}$+…+$\sqrt{2017}$-$\sqrt{2016}$)($\sqrt{2017}+1$)
=($\sqrt{2017}$-1)($\sqrt{2017}$+1)
=2017-1
=2016.
点评 本题考查的是分母有理化的应用,掌握平方差公式、二次根式的性质是解题的关键.


科目:初中数学 来源: 题型:解答题
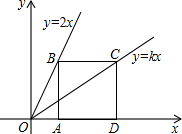 如图,已知四边形ABCD是正方形,点B,C分别在两条直线y=2x和y=kx上,点A,D是x轴上两点.
如图,已知四边形ABCD是正方形,点B,C分别在两条直线y=2x和y=kx上,点A,D是x轴上两点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在一幅长80cm,宽50cm的矩形风景画的四周镶一条金色纸边,制成一幅矩形挂图,如果要使整个挂图的面积是ycm2,设金色纸边的宽为xcm,要求纸边的宽度不得少于1cm,同时不得超过2cm.
在一幅长80cm,宽50cm的矩形风景画的四周镶一条金色纸边,制成一幅矩形挂图,如果要使整个挂图的面积是ycm2,设金色纸边的宽为xcm,要求纸边的宽度不得少于1cm,同时不得超过2cm.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,点A、B在数轴上,它们所对应的数分别是$\frac{2}{x-2}$和$\frac{1-x}{2-x}$.
如图,点A、B在数轴上,它们所对应的数分别是$\frac{2}{x-2}$和$\frac{1-x}{2-x}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,一种某小区的两幢10层住宅楼间的距离为AC=30m,由地面向上依次为第1层、第2层、…、第10层,每层高度为3m.假设某一时刻甲楼在乙楼侧面的影长EC=h,太阳光线与水平线的夹角为α.
如图,一种某小区的两幢10层住宅楼间的距离为AC=30m,由地面向上依次为第1层、第2层、…、第10层,每层高度为3m.假设某一时刻甲楼在乙楼侧面的影长EC=h,太阳光线与水平线的夹角为α.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 将长为20cm,宽为8cm的长方形白纸,按如图所示的方法粘合起来,粘合部分的宽为3cm,设x张白纸粘合后的总长度为ycm,y与x的函数关系式为y=17x+3.
将长为20cm,宽为8cm的长方形白纸,按如图所示的方法粘合起来,粘合部分的宽为3cm,设x张白纸粘合后的总长度为ycm,y与x的函数关系式为y=17x+3.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com