
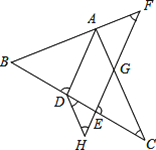
【题目】如图,AD平分∠BAC交BC于点D,点F在BA的延长线上,点E在线段CD上,EF与AC相交于点G,∠BDA+∠CEG=180°.
(1)AD与EF平行吗?请说明理由;
(2)若点H在FE的延长线上,且∠EDH=∠C,则∠F与∠H相等吗,请说明理由.
【答案】见解析
【解析】分析:(1)求出∠ADE+∠FEB=180°,根据平行线的判定推出即可;
(2)根据角平分线定义得出∠BAD=∠CAD,推出HD∥AC,根据平行线的性质得出∠H=∠CGH,∠CAD=∠CGH,推出∠BAD=∠F即可.
详解:(1)AD∥EF.
理由如下:∵∠BDA+∠CEG=180°,∠ADB+∠ADE=180°,∠FEB+∠CEF=180°
∴∠ADE+∠FEB=180°,∴AD∥EF;
(2)∠F=∠H,理由是:
∵AD平分∠BAC,∴∠BAD=∠CAD.
∵∠EDH=∠C,∴HD∥AC,∴∠H=∠CGH.
∵AD∥EF,∴∠CAD=∠CGH,∴∠BAD=∠F,∴∠H=∠F.


科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2﹣(m+2)x+(2m﹣1)=0.
(1)求证:方程恒有两个不相等的实数根;
(2)若此方程的一个根是1,请求出方程的另一个根,并求以此两根为边长的直角三角形的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次机器人测试中,要求机器人从A出发到达B处.如图1,已知点A在O的正西方600cm处,B在O的正北方300cm处,且机器人在射线AO及其右侧(AO下方)区域的速度为20cm/秒,在射线AO的左侧(AO上方)区域的速度为10cm/秒. 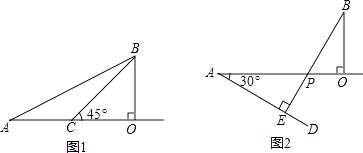
(参考数据: ![]() ≈1.414,
≈1.414, ![]() ≈1.732,
≈1.732, ![]() ≈2.236,
≈2.236, ![]() ≈2.449)
≈2.449)
(1)分别求机器人沿A→O→B路线和沿A→B路线到达B处所用的时间(精确到秒);
(2)若∠OCB=45°,求机器人沿A→C→B路线到达B处所用的时间(精确到秒);
(3)如图2,作∠OAD=30°,再作BE⊥AD于E,交OA于P.试说明:从A出发到达B处,机器人沿A→P→B路线行进所用时间最短.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线C:y=ax2+bx+c(a<0)过原点,与x轴的另一个交点为B(4,0),A为抛物线C的顶点. 
(1)如图1,若∠AOB=60°,求抛物线C的解析式;
(2)如图2,若直线OA的解析式为y=x,将抛物线C绕原点O旋转180°得到抛物线C′,求抛物线C、C′的解析式;
(3)在(2)的条件下,设A′为抛物线C′的顶点,求抛物线C或C′上使得PB=PA′的点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,BC=a,AC=b,AB=c,设c为最长边,当a2+b2=c2时,△ABC是直角三角形;当a2+b2≠c2时,利用代数式a2+b2和c2的大小关系,探究△ABC的形状(按角分类).
(1)当△ABC三边分别为6、8、9时,△ABC为 三角形;当△ABC三边分别为6、8、11时,△ABC为 三角形.
(2)猜想,当a2+b2 c2时,△ABC为锐角三角形;当a2+b2 c2时,△ABC为钝角三角形.
(3)判断当a=2,b=4时,△ABC的形状,并求出对应的c的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂现有甲种原料360千克,乙种原料290千克,计划利用这两种原料生产A、B两种产品50件.生产一件A产品需要甲种原料9千克,乙种原料3千克,可获利润700元;生产一件B产品,需要甲种原料4千克,乙种原料10千克,可获利润1200元.
(1)设生产x件A种产品,写出其题意x应满足的不等式组;
(2)由题意有哪几种按要求安排A、B两种产品的生产件数的生产方案?请您帮助设计出来.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com