
 如图,抛物线y=ax2+bx+c的开口向下,与x轴和y轴分别交于点A(-4,0)和点B(0,2),过点B作BC⊥AB交抛物线于点C,连接AC,且∠BAC=∠BAO.
如图,抛物线y=ax2+bx+c的开口向下,与x轴和y轴分别交于点A(-4,0)和点B(0,2),过点B作BC⊥AB交抛物线于点C,连接AC,且∠BAC=∠BAO.分析 (1)根据勾股定理,可得AB的长,根据相似三角形的判定与性质,可得答案;
(2)根据两点间的距离,可得两个方程,根据解方程,可得C点坐标,根据待定系数法,可得函数解析式;
(3)根据线段垂直平分线的性质,可得P在线段AB的垂直平分线上,根据线段垂直平分线的关系,可得AB的线段垂直平分线,根据解方程组,可得P点坐标.
解答 解:(1)在Rt△AOB中,由勾股定理,得
AB=$\sqrt{A{O}^{2}+O{B}^{2}}$=2$\sqrt{5}$.
∵BC⊥AB,
∴∠ABC=∠AOB=90°,
∵∠CAB=∠BAO,
∴△CAB∽△BAO,
∴$\frac{BC}{BO}$=$\frac{AB}{AO}$,即$\frac{BC}{2}$=$\frac{2\sqrt{5}}{4}$,
BC=$\sqrt{5}$;
(2)设C点坐标为(m,n),由勾股定理,
AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=5.
AC2=25,BC2=5,即$\left\{\begin{array}{l}{(m+4)^{2}+{n}^{2}=25}\\{{m}^{2}+(n-2)^{2}=5}\end{array}\right.$,
解得m=-1,m=1(舍),n=4,
即C点坐标(-1,4).
将A,B,C点坐标代入函数解析式,得
$\left\{\begin{array}{l}{a-b+c=4}\\{16a-4b+c=0}\\{c=2}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=-\frac{5}{6}}\\{b=-\frac{17}{6}}\\{c=2}\end{array}\right.$,
抛物线的解析式为y=-$\frac{5}{6}$x2-$\frac{17}{6}$x+2;
(3)AB的解析式为y=$\frac{1}{2}$x+2,AB的中点坐标为(-2,1),
AB的垂直平分线为y=-2x+b,将(-2,1)代入,解得b=-3,
AB的垂直平分线为y=-2x-3,
联立AB的垂直平分线与抛物线,得
$\left\{\begin{array}{l}{y=-\frac{5}{6}{x}^{2}-\frac{17}{6}x+2}\\{y=-2x-3}\end{array}\right.$,
解得$\left\{\begin{array}{l}{{x}_{1}=\frac{3}{2}}\\{{y}_{1}=-6}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=-\frac{7}{2}}\\{{y}_{2}=4}\end{array}\right.$,
抛物线上存在点P,使得PA=PB,P点坐标为($\frac{3}{2}$,-6),(-$\frac{7}{2}$,4).
点评 本题考查了二次函数综合题,解(1)的关键是利用相似三角形的判定与性质;解(2)的关键是利用两点间的距离求出C点坐标,又利用了待定系数法;解(3)的关键是确定P是AB的垂直平分线与抛物线的交点,又利用了解方程组.


科目:初中数学 来源: 题型:解答题
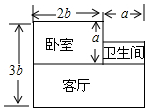 小张刚搬进一套新房子,如图所示(单位:m),他打算把客厅铺上地砖
小张刚搬进一套新房子,如图所示(单位:m),他打算把客厅铺上地砖查看答案和解析>>
科目:初中数学 来源: 题型:解答题
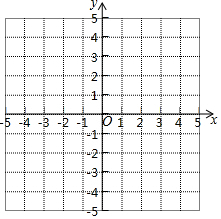 请按要求画出函数y=$\frac{1}{2}$x2的图象:
请按要求画出函数y=$\frac{1}{2}$x2的图象:| x | … | -3 | -2 | -1 | 0 | 1 | 2 | 3 | … |
| y | … | $\frac{9}{2}$ | 2 | $\frac{1}{2}$ | 0 | $\frac{1}{2}$ | 2 | $\frac{9}{2}$ | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
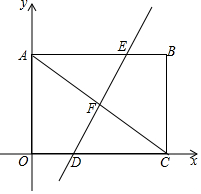 如图,平面直角坐标系中,矩形OABC的对角线AC=10,边OA=6.
如图,平面直角坐标系中,矩形OABC的对角线AC=10,边OA=6.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
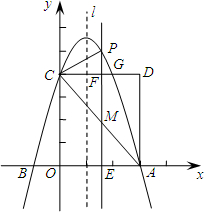 如图所示,在矩形OADC中,以点O为原点,以OA,OC所在直线分别为x轴,y轴建立平面直角坐标系,且抛物线y=-x2+bx+c与x轴交于点A,与y轴交于点C,且D点的坐标为(6,8).
如图所示,在矩形OADC中,以点O为原点,以OA,OC所在直线分别为x轴,y轴建立平面直角坐标系,且抛物线y=-x2+bx+c与x轴交于点A,与y轴交于点C,且D点的坐标为(6,8).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
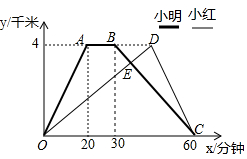 小明和小红同时从学校出发骑自行车到公园后返回,他们与学校的距离y(千米)和离开学校的时间x(分钟)之间的关系如图.
小明和小红同时从学校出发骑自行车到公园后返回,他们与学校的距离y(千米)和离开学校的时间x(分钟)之间的关系如图.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com