
�� �֣�������
�֣������� �У�
��  ��
�� 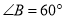 ����
���� ���߶�
���߶� �ϵ�һ�����㣮
�ϵ�һ�����㣮
�� ����ͼ�٣���
����ͼ�٣��� ����Сֵ��
����Сֵ��
��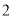 ����ͼ�ڣ���
����ͼ�ڣ��� Ҳ��
Ҳ�� ���ϵ�һ�����㣬��
���ϵ�һ�����㣬�� ����
���� ����Сֵ��
����Сֵ��
�� ����ͼ�ۣ���
����ͼ�ۣ���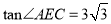 �����������ڲ�����һ��
�����������ڲ�����һ�� ��ʹ�õ�
��ʹ�õ�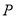 �ֱ�
�ֱ� ����
���� ����
���� �ľ���֮����С�����㻭�������ĵ�
�ľ���֮����С�����㻭�������ĵ� ������������Сֵ��
������������Сֵ��


 ����С����ͬ������ϵ�д�
����С����ͬ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ��2017-2018ѧ�����꼶��ѧ�˽̰��ϲ��4�� ����ͼ�γ��� ��Ԫ���Ծ� ���ͣ������
��֪�߶�AB��20cm��M���߶�AB���е㣬C���߶�AB�ӳ����ϵĵ㣬AC��BC��3��1����D���߶�BA�ӳ����ϵĵ㣬AD��AB.��
(1)�߶�BC�ij���
(2)�߶�DC�ij���
(3)�߶�MD�ij���
��1��10����2��50����3��30. �������������������1����BC��xcm����AC��3xcm������AC��AB��BC��(20��x)cm���ɵ÷�20��x��3x���ⷽ�̼������BC��ֵ����2����DC��AD��AB��BC�������DC�ij�����3�������е�Ķ������AM�ij�������MD��AD��AM�������MD�ij�. ��������� (1)��BC��xcm����AC��3xcm. �֡�AC��AB��B...�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2017-2018ѧ��ɽ��ʡ��������У���꼶���ϣ���һ��������ѧ�Ծ� ���ͣ���ѡ��
һ���칫������5յ�ƣ�������40W��60W���ֵ��ݣ��ܵ�����Ϊ260W����40W��60W�ĵ��ݸ����ֱ�Ϊ�� ��
A. 1��4 B. 2��3 C. 3��2 D. 4��1
B ����������40w�ĵ����и���������ɵã� �� ��ã� �� �࣬ ��40w�ĵ�����2����60w�ĵ�����3��. ��ѡB.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ������2017-2018ѧ����ѧ����ĩ��ѧ���������꼶��ѧ�Ծ� ���ͣ���ѡ��
ij��Ϊ�������������ƻ�����ͼ��ʾ�������οյ�����ֲ��Ƥ����֪���ֲ�Ƥÿƽ�����ۼ�ΪaԪ���������ֲ�Ƥ������Ҫ��������

A. 450aԪ B. 225aԪ C. 150aԪ D. 300aԪ
C �������������������ͼ����BA�ߵĸ�CD������BA���ӳ��߽��ڵ�D�� �ߡ�BAC=150�㣬 ���DAC=30�㣬 ��CD��BD��AC=30m�� ��CD=15m�� ��AB=20m�� ��S��ABC=AB��CD=��20��15=150m2�� ��ÿƽ�����ۼ�aԪ�� ������ֲ�Ƥ�ļ۸�Ϊ150aԪ�� ��ѡC.�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ������2017-2018ѧ����ѧ����ĩ��ѧ���������꼶��ѧ�Ծ� ���ͣ������
��ͼ�����߳�Ϊ6cm��������ABCD�۵���ʹ��D����AB�ߵ��е�E�����ۺ�ΪFH����C����Q����EQ��BC���ڵ�G�����EBG���ܳ��� cm��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ2018����꼶��ѧ�����п�����ѧ�Ծ� ���ͣ������
���������� �֣�С����С����һ����¥ǰ�п�¥����ߣ�С��˵������¥����
�֣�С����С����һ����¥ǰ�п�¥����ߣ�С��˵������¥���� �㣡��С��ȴ����ΪȻ����
�㣡��С��ȴ����ΪȻ���� �㣿�ҿ�û�У���С��˵�����б��£���������һ���������ɣ���
�㣿�ҿ�û�У���С��˵�����б��£���������һ���������ɣ���
��ͼ������ ��ʾ¥�壬С����С����¥�������ѡ
��ʾ¥�壬С����С����¥�������ѡ ��
�� ���㣬ʹ��
���㣬ʹ�� ��
�� ��
�� ��
�� �ĵ���ͬһֱ���ϣ�����Ƥ�ߺͲ���������������ݣ�
�ĵ���ͬһֱ���ϣ�����Ƥ�ߺͲ���������������ݣ�  �ף�
�ף�  �ף�
�ף�  ��
��  ��
��

�� ���������������һ��¥�ߣ�������������ţ�
���������������һ��¥�ߣ�������������ţ�
�� ����ÿ��¥��
����ÿ��¥�� ���㣬��֧��С������С���Ĺ۵��أ���˵�����ɣ�
���㣬��֧��С������С���Ĺ۵��أ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ʡ2018����꼶��ѧ�����п�����ѧ�Ծ� ���ͣ������
��ͼ��  ��
�� ��˫�����ϵ����㣬��
��˫�����ϵ����㣬�� ����
����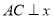 ���ڵ�
���ڵ� ����
���� �ڵ�
�ڵ� ����
���� �����Ϊ
�����Ϊ ��
�� 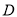 Ϊ
Ϊ ���е㣬��
���е㣬��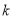 ��ֵΪ__________��
��ֵΪ__________��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���˽̰���꼶�꼶��ѧ�²�ڶ�ʮ���� ������ ���ͣ������
��ͼ���۲����ⳤΪ1��С������ڳɵ�ͼ�Σ�Ѱ�ҹ��ɣ���ͼ���У�����1��С�����壬����1�����ü���0������������ͼ���У�����8��С�����壬����7�����ü���1������������ͼ���У�����27��С�����壬����19�����ü���8����������������ڢ�ͼ�У����ü���С��������_____����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ���˽̰����꼶�²���ѧ�������ཻ����ƽ���ߵ�Ԫ���� ���ͣ������
��ͼ��EF��AD����1=��2����BAC=70�㣬

��1��DGƽ��AB����˵������.
��2�����AGD�Ķ�����
��1������������2��110�� ����������������� ��1��ֻ���жϳ���1���3��һ���ڴ����Ƿ���ȼ��ɣ� ��2����AGD���ABCΪͬ���ڽǣ��ɣ�1��֪DG//AB,l����ƽ�������ʼ��������AGD. �������� ��1��DGƽ��AB. ���ɣ���EF��AD�� ���2=��3�� �ߡ�1=��2�� ���1=��3�� ��DG��AB�� ��2���������� ��DG��...�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com