
分析 利用条件和因式分解可得:0≤(a-2)2+(b-3)2+(c-6)2<1,即a=2,b=3,c=6,然后代入原式即可求出答案.
解答 解:∵a2+b2+c2+49-4a-6b-12c<1,
∴(a-2)2+(b-3)2+(c-6)2<1,
∵(a-2)2≥0,(b-3)2≥0,(c-6)2≥0,
∴0≤(a-2)2+(b-3)2+(c-6)2<1,
∵a、b、c为整数,
∴(a-2)2+(b-3)2+(c-6)2也是整数,
∴(a-2)2+(b-3)2+(c-6)2=0,
∴a=2,b=3,c=6,
∴原式=($\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{6}$)36=1
点评 本题考查分式化简求值,涉及因式分解,不等式的性质等知识,综合程度较高.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:填空题
 如图,直线y=x+t和抛物线y=x2+bx+c相交于A(1,0),B(4,3)两点,则t的值为-1,不等式x2+(b-1)x+c-t>0的解集为x<1或x>4.
如图,直线y=x+t和抛物线y=x2+bx+c相交于A(1,0),B(4,3)两点,则t的值为-1,不等式x2+(b-1)x+c-t>0的解集为x<1或x>4.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
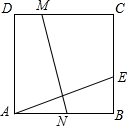 如图所示,四边形ABCD是边长为3的正方形,E是BC边上一点,且EC=2BE,将正方形折叠,使点A与点E重合,折痕为MN,若四边形BCMN的面积和四边形ADMN的面积分别为S1,S2.求S1:S2.
如图所示,四边形ABCD是边长为3的正方形,E是BC边上一点,且EC=2BE,将正方形折叠,使点A与点E重合,折痕为MN,若四边形BCMN的面积和四边形ADMN的面积分别为S1,S2.求S1:S2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com