
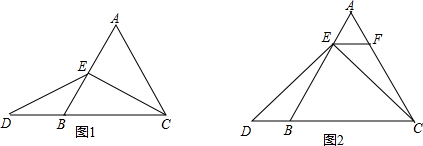
���� ��1���ɵȱ������ε����ʵó���ABC=��ACB=60�㣬��BCE=30�㣬��֤����BED=��D���ó�BE=DB�����ɵó�AE=DB��
��2���ɵȱ������ε����ʵó���ABC=��ACB=��A=60�㣬��DBE=120�㣬��֤����AEF�ǵȱ������Σ��ó�AE=EF��BE=CF��֤����FEC=��D��֤����EFC�ա�DBE���ó�EF=DB�����ɵó�AE=DB��
��3���ɣ�2����֪AE=DB=2����ΪBC=10���������CD=12��8��
��� 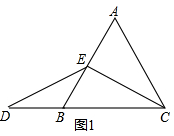 �⣺��1��AE=DB���������£�
�⣺��1��AE=DB���������£�
�ߡ�ABC�ǵȱ������Σ���EΪAB���е㣬
���ABC=��ACB=60�㣬��BCE=$\frac{1}{2}$��ACB=30�㣬AE=BE��
��ED=EC��
���D=��BCE=30�㣬
�ߡ�ABC=��D+��BED��
���BED=30��=��D��
��BE=DB��
��AE=DB��
�ʴ�Ϊ��=��
��2��AE=DB���������£�
����E��EF��BC����AC�ڵ�F����ͼ2��ʾ��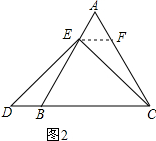
�ߡ�ABC�ǵȱ������Σ�
���ABC=��ACB=��A=60�㣬
���DBE=120�㣬
��EF��BC��
���AEF=��ABC����AFE=��ACB����FEC=��DCE��
���A=��AEF=��AFE=60�㣬
���AEF�ǵȱ������Σ���EFC=120�㣬
��AE=EF��
��BE=CF��
��ED=EC��
���D=��DCE��
���FEC=��D��
�ڡ�EFC�͡�DBE�У�
$\left\{\begin{array}{l}{��EFC=��DBE=120��}\\{��FEC=��D}\\{CF=BD}\end{array}\right.$��
���EFC�ա�DBE��AAS����
��EF=DB��
��AE=DB��
�ʴ�Ϊ��=��
��3���ߡ�ABC�ı߳�Ϊ10��AE=2��
��BC=10��
�ɣ�2����֪AE=DB��
��DB=2��
�൱E���߶�AB��ʱ��CD=DB+BC=2+10=12��
��E������BA��ʱ��CD=BC-DB=10-2=8��
���� ���⿼���˵ȱ������ε��������ж���ȫ�������ε��ж������ʡ����������ε����ʣ�������һ���Ѷȣ��ر��ǣ�2���У���Ҫͨ����������֤���ȱ������κ�ȫ�������β��ܵó����ۣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 5 | B�� | 6 | C�� | -5 | D�� | -6 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1080 | B�� | 1440 | C�� | 1620 | D�� | 1800 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
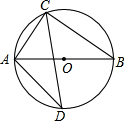 ��֪���ڡ�O�У�ֱ��AB�ij�Ϊ10cm����AC�ij�Ϊ6cm����ACB��ƽ���߽���O�ڵ�D��
��֪���ڡ�O�У�ֱ��AB�ij�Ϊ10cm����AC�ij�Ϊ6cm����ACB��ƽ���߽���O�ڵ�D���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��֪���κ���y=$\frac{1}{2}$x2+3x+2��ͼ����x�ύ��A��B���㣬��y�ύ��D�㣬����ΪC�����ı���ACBD�������
��֪���κ���y=$\frac{1}{2}$x2+3x+2��ͼ����x�ύ��A��B���㣬��y�ύ��D�㣬����ΪC�����ı���ACBD��������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com