
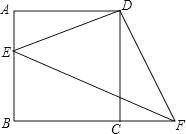
【题目】如图,四边形ABCD是正方形,E点在AB上,F点在BC的延长线上,且CF=AE,连接DE、DF、EF.
①求证:△ADE≌△CDF;
②填空:△CDF可以由△ADE绕旋转中心 点,按逆时针方向旋转 度得到;
③若BC=3,AE=1,求△DEF的面积.
【答案】(1)详见解析;(2)D,90;
【解析】
试题分析:(1)根据SAS即可证得;(2)根据旋转的定义即可解答;(3)根据S△BEF=S梯形ABFD﹣S△ADE﹣S△BEF即可求解.
试题解析:(1)证明:∵正方形ABCD中,∠A=∠BCD=90°,则∠DCF=∠A=90°,AD=CD,
在△ADE和△CDF中,
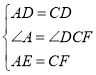 ,
,
∴△ADE≌△CDF;
(2)△CDF可以由△ADE绕旋转中心D点,按逆时针方向旋转90度得到.
(3)AD=AB=BC=3,CF=AE=1,
则S梯形ABFD=![]() (AD+BF)AB=
(AD+BF)AB=![]() ×(3+4)×3=18,
×(3+4)×3=18,
S△ADE=![]() AEAD=
AEAD=![]() ×1×3=
×1×3=![]() ;
;
S△BEF=![]() BEBF=
BEBF=![]() ×2×(3+1)=4,
×2×(3+1)=4,
则S△DEF=18﹣![]() ﹣4=
﹣4=![]() .
.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,⊙O的半径为1,P是坐标系内任意一点,点P到⊙O的距离SP的定义如下:若点P与圆心O重合,则SP为⊙O的半径长;若点P与圆心O不重合,作射线OP交⊙O于点A,则SP为线段AP的长度.
图1为点P在⊙O外的情形示意图.
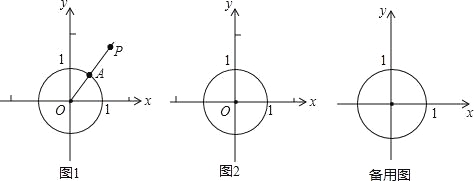
(1)若点B(1,0),C(1,1),D(0,![]() ),则SB= ;SC= ;SD= ;
),则SB= ;SC= ;SD= ;
(2)若直线y=x+b上存在点M,使得SM=2,求b的取值范围;
(3)已知点P,Q在x轴上,R为线段PQ上任意一点.若线段PQ上存在一点T,满足T在⊙O内且ST≥SR,直接写出满足条件的线段PQ长度的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
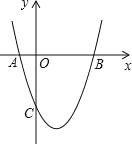
【题目】如图,抛物线y=x2+bx+c与x轴交于A(﹣1,0),B(3,0)两点.
(1)求该抛物线的解析式;
(2)求该抛物线的对称轴以及顶点坐标;
(3)设(1)中的抛物线上有一个动点P,当点P在该抛物线上滑动到什么位置时,满足S△PAB=8,并求出此时P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数的图象经过点(0,﹣3),(2,5),(﹣1,﹣4)且与x轴交于A、B两点,其顶点为P.
(1)试确定此二次函数的解析式;
(2)根据函数的图象,指出函数的增减性,并直接写出函数值y<0时自变量x的取值范围.
(3)求△ABP的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了促进经济社会平衡发展,保障低收入群体生活水平不受疫情影响,郑州市人民政府计划向社会发放近4亿消费券,如今第一期消费券已于4月3日上午10点准时发放,总额5000万元,请将5000万用科学记数法表示为( )
A.5×103B.5×107C.5×104D.5×108
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,并且关于x的一元二次方程ax2+bx+c﹣m=0有两个不相等的实数根,下列结论:
①b2﹣4ac<0;②abc>0;③a﹣b+c<0;④m>﹣2,
其中,正确的个数有( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读对话,解答问题:

(1)分别用a、b表示小冬从小丽、小兵袋子中抽出的卡片上标有的数字,请用树状图法或列表法写出(a,b)的所有取值;
(2)求在(a,b)中使关于x的一元二次方程x2﹣ax+2b=0有实数根的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是边长为5的等边三角形,△BDC是顶角为120°的等腰三角形,以D为顶点作一个60°的∠MDN,点M、N分别在AB、AC上,连接MN,则△AMN的周长为 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com