
【题目】如图,在平面直角坐标系中,抛物线y=﹣![]() x2+bx+c,经过A(0,﹣4),B(x1 , 0),C(x2 , 0)三点,且|x2﹣x1|=5.
x2+bx+c,经过A(0,﹣4),B(x1 , 0),C(x2 , 0)三点,且|x2﹣x1|=5.
(1)求b,c的值;
(2)在抛物线上求一点D,使得四边形BDCE是以BC为对角线的菱形;
(3)在抛物线上是否存在一点P,使得四边形BPOH是以OB为对角线的菱形?若存在,求出点P的坐标,并判断这个菱形是否为正方形?若不存在,请说明理由.
【答案】
(1)
【解答】解:∵抛物线y=﹣![]() x2+bx+c,经过点A(0,﹣4),
x2+bx+c,经过点A(0,﹣4),
∴c=﹣4
又∵由题意可知,x1、x2是方程﹣![]() x2+bx﹣4=0的两个根,
x2+bx﹣4=0的两个根,
∴x1+x2=![]() b,x1x2=6
b,x1x2=6
由已知得(x2﹣x1)2=25
又∵(x2﹣x1)2=(x2+x1)2﹣4x1x2=![]() b2﹣24
b2﹣24
∴![]() b2﹣24=25
b2﹣24=25
解得b=±![]() ,当b=
,当b=![]() 时,抛物线与x轴的交点在x轴的正半轴上,不合题意,舍去.
时,抛物线与x轴的交点在x轴的正半轴上,不合题意,舍去.
∴b=﹣![]() .
.
(2)
∵四边形BDCE是以BC为对角线的菱形,根据菱形的性质,点D必在抛物线的对称轴上,
又∵y=﹣![]() x2﹣
x2﹣![]() x﹣4=﹣
x﹣4=﹣![]() (x+
(x+![]() )2+
)2+![]() ,
,
∴抛物线的顶点(﹣![]() ,
,![]() )即为所求的点D.
)即为所求的点D.
(3)
∵四边形BPOH是以OB为对角线的菱形,点B的坐标为(﹣6,0),根据菱形的性质,点P必是直线x=﹣3与
抛物线y=﹣![]() x2﹣
x2﹣![]() x﹣4的交点,
x﹣4的交点,
∴当x=﹣3时,y=﹣![]() ×(﹣3)2﹣
×(﹣3)2﹣![]() ×(﹣3)﹣4=4,
×(﹣3)﹣4=4,
∴在抛物线上存在一点P(﹣3,4),使得四边形BPOH为菱形.
四边形BPOH不能成为正方形,因为如果四边形BPOH为正方形,点P的坐标只能是(﹣3,3),但这一点不在抛物线上.
【解析】(1)把A(0,﹣4)代入可求c,运用两根关系及|x2﹣x1|=5,对式子合理变形,求b;
(2)因为菱形的对角线互相垂直平分,故菱形的另外一条对角线必在抛物线的对称轴上,满足条件的D点,就是抛物线的顶点;
(3)由四边形BPOH是以OB为对角线的菱形,可得PH垂直平分OB,求出OB的中点坐标,代入抛物线解析式即可,再根据所求点的坐标与线段OB的长度关系,判断是否为正方形即可.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图1,水平放置一个三角板和一个量角器,三角板的边AB和量角器的直径DE在一条直线上,AB=BC=6cm,OD=3cm,开始的时候BD=1cm,现在三角板以2cm/s的速度向右移动.
(1)当B与O重合的时候,求三角板运动的时间;
(2)如图2,当AC与半圆相切时,求AD;
(3)如图3,当AB和DE重合时,求证:CF2=CGCE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义运算max{a,b}:当a≥b时,max{a,b}=a;当a<b时,max{a,b}=b.如max{﹣3,2}=2.
(1)max{![]() ,3}= ;
,3}= ;
(2)已知y1=![]() 和y2=k2x+b在同一坐标系中的图象如图所示,若max{
和y2=k2x+b在同一坐标系中的图象如图所示,若max{![]() ,k2x+b}=
,k2x+b}=![]() ,结合图象,直接写出x的取值范围;
,结合图象,直接写出x的取值范围;
(3)用分类讨论的方法,求max{2x+1,x﹣2}的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班同学响应“阳光体育运动”号召,利用课外活动积极参加体育锻炼,每位同学从长跑、铅球、立定跳远、篮球定时定点投篮中任选一项进行了训练,训练前后都进行了测试,现将项目选择情况及训练后篮球定时定点投篮进球数进行整理,作出如下统计图表.
训练后篮球定点投篮测试进球统计表
进球数(个) | 8 | 7 | 6 | 5 | 4 | 3 |
人数 | 2 | 1 | 4 | 7 | 8 | 2 |
请你根据图表中的信息回答下列问题:
(1)训练后篮球定时定点投篮人均进球数为 个;
(2)选择长跑训练的人数占全班人数的百分比是 ,该班共有同学 人;
(3)根据测试资料,参加篮球定时定点投篮的学生训练后比训练前的人均进球增加了25%,求参加训练之前的人均进球数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,A,C分别在坐标轴上,点B的坐标为(4,2),直线y=﹣![]() x+3交AB,BC于点M,N,反比例函数y=
x+3交AB,BC于点M,N,反比例函数y=![]() 的图象经过点M,N.
的图象经过点M,N.
(1)求反比例函数的解析式;
(2)若点P在x轴上,且△OPM的面积与四边形BMON的面积相等,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在10×10的正方形网格中,点A,B,C,D均在格点上,以点A为位似中心画四边形AB′C′D′,使它与四边形ABCD位似,且相似比为2.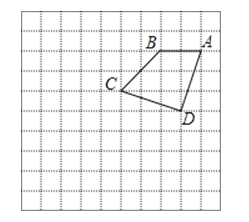
(1)在图中画出四边形AB′C′D′;
(2)填空:△AC′D′是 三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校在基地参加社会实践话动中,带队老师考问学生:基地计划新建一个矩形的生物园地,一边靠旧墙(墙足够长),另外三边用总长69米的不锈钢栅栏围成,与墙平行的一边留一个宽为3米的出入口,如图所示,如何设计才能使园地的而积最大?下面是两位学生争议的情境:
请根据上面的信息,解决问题:
(1)设AB=x米(x>0),试用含x的代数式表示BC的长
(2)请你判断谁的说法正确,为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,顶点为A(1,﹣1)的抛物线经过点B(5,3),且与x轴交于C,D两点(点C在点D的左侧).
(1)求抛物线的解析式;
(2)求点O到直线AB的距离;
(3)点M在第二象限内的抛物线上,点N在x轴上,且∠MND=∠OAB,当△DMN与△OAB相似时,请你直接写出点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AC为直径的⊙O交AB于点D,交BC于点E. 
(1)求证:BE=CE;
(2)若BD=2,BE=3,求AC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com