练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，位于A处的海上救援中心获悉：在其北偏东68°方向的B处有一艘渔船遇险，在原地等待营救．该中心立即把消息告知在其北偏东30°且距离A点20海里的C处救生船，此时，遇险船在救生船的正东方向B处，现救生船沿着航线CB前往B处救援，求救生船到达B处行驶的距离？（参考数据：sin68°≈0.90，cos68°≈0.36，tan68°≈2.50，≈1.7）


    解：如图，延长BC交AN于点D，则BC⊥AN于D．

    在Rt△ACD中，∵∠ADC=90°，∠DAC=30°，

    ∴DC=AC=10，AD=CD=10≈17．

    在Rt△ABD中，∵∠ADB=90°，∠DAB=68°，

    ∴tan68°=            

    ∴BD≈17×2.50=42.5，               

    ∴BC=BD﹣CD≈42.5﹣10=32.5，            


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    如图，△ABC≌△BAD， AC与BD是对应边，AC=8cm，CB=10cm，DE=3cm，那么AE的长

    是（　　）．

    A．10cm           B．8cm         C．7cm        D．5cm

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    在数轴上画出表示下列各数的点，并把它们按从小到大的

    顺序用“<”连接起来：-3，3.5，0，-，-4，1.5

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    在反比例函数中，当x＞0时，y随x的增大而增大，则二次函数图像大致是（　　）

    查看答案和解析>>

    科目：初中数学 来源： 题型：


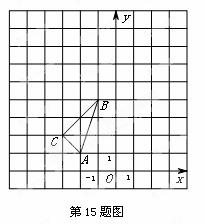
    如图，在平面直角坐标系中，的三个顶点坐标分别为(，1)，(，4)，(，2)．以原点为位似中心，位似比为1:2，在轴的左侧，

    画出放大后的图形，并直接写出点坐标；

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，在Rt△ABC中，∠C=90°，AC=4cm，BC=3cm．动点M从点C出发，以每秒1cm的速度沿CA向终点A移动，同时动点P从点A出发，以每秒2cm的速度沿AB向终点B移动，连接PM，设移动时间为t（s）（0＜t＜2.5）．

    （1）当AP=AM时，求t的值.

    （2）设四边形BPMC的面积为（cm²），求y与t之间的函数关系式；

    （3）是否存在某一时刻t，使四边形BPMC的面积是Rt△ABC面积的？若存在，求出相应t的值，若不存在，说明理由；

    （4）是否存在某一时刻t，使以M，P，A为顶点的三角形与△ABC相似？若存在，求出相应t的值;若不存在，说明理由.

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，一个小球由地面沿着坡度的坡面向上前进了10 m，此时小球距离地面的高度为(    )

    A.            B.2 m        C.4 m        D.m

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图所示，一条渔船某时刻在位置A观测灯塔B、C(灯塔B距离A处较近)，两个灯塔恰好在北偏东65°45′的方向上，渔船向正东方向航行1小时45分钟之后到达D点，观测到灯塔B恰好在正北方向上，在图中作CE⊥AD.已知两个灯塔之间的距离是12海里，渔船的速度是16海里／时，又知在灯塔C周围18.6海里内有暗礁，问这条渔船按原来的方向续航行，有没有触礁的危险?

     


    查看答案和解析>>

    科目：初中数学 来源： 题型：


    在△ABC中，已知AC＝，BC＝，AB＝3，那么sin A＝_______．

    查看答案和解析>>

    同步练习册答案