
 已知:如图,菱形ABCD的对角线AC,BD相交于O,点E,F分别是AD,DC的中点.已知OE=$\frac{5}{2}$,EF=3,求菱形ABCD的周长和面积.
已知:如图,菱形ABCD的对角线AC,BD相交于O,点E,F分别是AD,DC的中点.已知OE=$\frac{5}{2}$,EF=3,求菱形ABCD的周长和面积. 分析 首先由菱形ABCD的对角线AC,BD相交于O,点E,F分别是AD,DC的中点,根据直角三角形斜边上的中线等于斜边的一半,可求得AB的长,由三角形中位线定理可求得AC的长,进而可求出菱形的周长,再求出AC的长即可求出菱形的面积.
解答 解:∵菱形ABCD的对角线AC,BD相交于点O,
∴AC⊥BD,OA=OC,OB=OD,
∵点E,F分别是AD,DC的中点,
∴OE=$\frac{1}{2}$AB,EF=$\frac{1}{2}$AC,
∵OE=$\frac{5}{2}$,EF=3,
∴AB=5,AC=6,
∴菱形ABCD的周长为:4×5=20;
∵AO=$\frac{1}{2}$AC=3,AB=5,
∴BO=$\sqrt{A{B}^{2}-O{A}^{2}}$=4,
∴BD=2BO=8,
∴菱形ABCD的面积为:$\frac{1}{2}$AC•BD=24.
点评 此题考查了菱形的性质、三角形中位线的性质、勾股定理以及直角三角形的性质.注意根据题意求得AC与AB的长是解此题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
 如图,在?ABCD中,对角线AC、BD相交于点O,且OA=OB,若AD=4,∠AOD=60°,则AB的长为( )
如图,在?ABCD中,对角线AC、BD相交于点O,且OA=OB,若AD=4,∠AOD=60°,则AB的长为( )| A. | 4$\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | 8 | D. | 8$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3$\sqrt{2}$-2$\sqrt{3}$=1 | B. | $\root{3}{-27}$=-3 | C. | |$\sqrt{2}$-$\sqrt{3}$|+$\sqrt{2}$=2$\sqrt{2}$-$\sqrt{3}$ | D. | ($\sqrt{3}$+$\frac{1}{\sqrt{3}}$)÷$\sqrt{3}$=4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 完成下面证明:如图,B是射线AD上一点,∠DAE=∠CAE,∠DAC=∠C=∠CBE
完成下面证明:如图,B是射线AD上一点,∠DAE=∠CAE,∠DAC=∠C=∠CBE查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
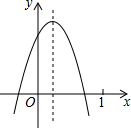 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:①b<0,c>0;②a+b+c<0;③方程ax2+bx+c=0的两根之和大于0;④a-b+c<0,其中正确的个数是( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:①b<0,c>0;②a+b+c<0;③方程ax2+bx+c=0的两根之和大于0;④a-b+c<0,其中正确的个数是( )| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,已知E、F、G、H分别为菱形ABCD四边的中点,AB=4cm,∠ABC=60°,则四边形EFGH的面积为4$\sqrt{3}$cm2.
如图,已知E、F、G、H分别为菱形ABCD四边的中点,AB=4cm,∠ABC=60°,则四边形EFGH的面积为4$\sqrt{3}$cm2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com