
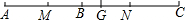 如图所示,G是线段AC的中点,点B在线段AC上,且M是线段AB的中点,N是线段BC的中点,那么下列等式成立的是( )
如图所示,G是线段AC的中点,点B在线段AC上,且M是线段AB的中点,N是线段BC的中点,那么下列等式成立的是( )| A. | MN=GC | B. | MG=$\frac{1}{2}$(AG-GB) | C. | GN=$\frac{1}{2}$(GC+GB) | D. | MN=$\frac{1}{2}$(AC+GB) |
分析 根据G是线段AC的中点,M是线段AB的中点,N是线段BC的中点,运用线段的和差关系进行判断即可.
解答 解:∵G是线段AC的中点,
∴GC=$\frac{1}{2}$AC,
∵M是线段AB的中点,N是线段BC的中点,
∴MB=$\frac{1}{2}$AB,NB=$\frac{1}{2}$BC,
∴MN=MB+NB=$\frac{1}{2}$(AB+BC)=$\frac{1}{2}$AC,
∴MN=GC,故A正确;
∵M是线段AB的中点,
∴MB=$\frac{1}{2}$AB=$\frac{1}{2}$(AG-GB)≠MG,故B错误;
∵N是线段BC的中点,
∴BN=$\frac{1}{2}$BC=$\frac{1}{2}$(GC+GB)≠GN,故C错误;
∵M是线段AB的中点,N是线段BC的中点,
∴MB=$\frac{1}{2}$AB,NB=$\frac{1}{2}$BC,
∴MN=MB+NB=$\frac{1}{2}$(AB+BC)=$\frac{1}{2}$AC≠$\frac{1}{2}$(AC+GB),故D错误;
故选:A.
点评 本题主要考查了两点间的距离以及中点定义的运用,解决问题的关键是灵活运用线段的和差关系进行判断.解题时注意:连接两点间的线段的长度叫两点间的距离.


 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案科目:初中数学 来源: 题型:选择题
| A. | 64的平方根是±4 | B. | -$\frac{1}{8}$没有立方根 | ||
| C. | 算术平方根等于本身的数是0 | D. | $\root{3}{-27}=-\root{3}{27}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 长方体、正方体都是棱柱 | |
| B. | 六棱柱有18条棱、6个侧面、12个顶点 | |
| C. | 三棱柱的侧面是三角形 | |
| D. | 圆柱由两个平面和一个曲面围成 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 近似数1.8与1.80表示的意义不一样 | |
| B. | 5.0万精确到万位 | |
| C. | 0.200精确到千分位 | |
| D. | 0.345×105用科学记数法表示为3.45×104 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
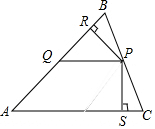 如图,在△ABC中,P是BC上的点,作PQ∥AC交AB于点Q,分别作PR⊥AB,PS⊥AC,垂足分别是R,S,若PR=PS,则下面三个结论:①AS=AR②AQ=PQ③△PQR≌△CPS,其中正确的是( )
如图,在△ABC中,P是BC上的点,作PQ∥AC交AB于点Q,分别作PR⊥AB,PS⊥AC,垂足分别是R,S,若PR=PS,则下面三个结论:①AS=AR②AQ=PQ③△PQR≌△CPS,其中正确的是( )| A. | ①③ | B. | ①② | C. | ②③ | D. | ①②③ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3.5<$\sqrt{11}$<3 | B. | $\sqrt{11}$<3.5<3 | C. | 3<$\sqrt{11}$<3.5 | D. | 3<3.5<$\sqrt{11}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
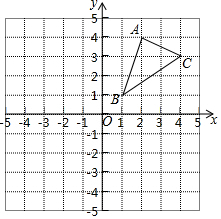 如图,△ABC三个顶点的坐标分别为A(2,4),B(1,1),C(4,3).
如图,△ABC三个顶点的坐标分别为A(2,4),B(1,1),C(4,3).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com