
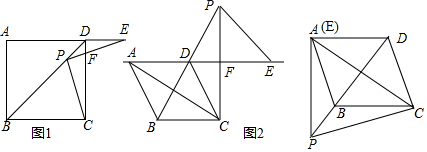
分析 (1)先证出△ADP≌△CDP,得PA=PC,再证明PA=PE,得PC=PE;
(2)①如图2中,设AC交BD于O.首先证明PC=PE=PA,由∠CPE=60°推出PC=PE=CE=AC=4,由四边形ABCD是菱形,推出AC⊥BD,根据BP=PO+OB计算即可;②如图3中,利用①中方法计算即可;
解答 (1)证明:如图1中,连接PA.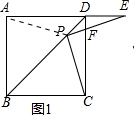
在正方形ABCD中,AD=DC,
∠ADP=∠CDP=45°,
在△ADP和△CDP中,
$\left\{\begin{array}{l}{DA=DC}\\{∠ADP=∠CDP}\\{DP=DP}\end{array}\right.$,
∴△ADP≌△CDP(SAS),
∴PA=PC,∠DAP=∠DCP,
∵∠CPF=∠EDF=90°,∠PFC=∠EFD,
∴∠PCF=∠E,
∴∠PAD=∠E
∴PA=PE,
∴PC=PE;
(2)①如图2中,设AC交BD于O,连接CE.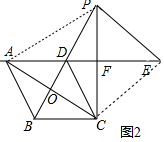
∵四边形ABCD是菱形,
∴∠ADO=∠CDO,
∴∠ADP=∠CDP,
∵DA=DC,DP=DP,
∴△ADP≌△CDP,
∴PA=PC,∠PAD=∠PCD,
∵∠CPE=∠CDF=60°,∠DFC=∠PFE,
∴∠E=∠PCD=∠PAD,
∴PA=PE=PC,
∴△PCE是等边三角形,
∴AC=CE=PE=PA=PC=4,
∵四边形ABCD是菱形,
∴AC⊥BD,
∴BP=PO+OB=2$\sqrt{3}$+$\frac{2}{\sqrt{3}}$=$\frac{8\sqrt{3}}{3}$
②如图3中,
利用①中方法可知PB=2$\sqrt{3}$-$\frac{2}{\sqrt{3}}$=$\frac{4\sqrt{3}}{3}$.
点评 本题考查菱形的性质、全等三角形的判定和性质、解直角三角形等知识,解题的关键是灵活运用所学知识解决问题,学会用分类讨论的思想思考问题,属于中考常考题型.


科目:初中数学 来源: 题型:解答题
| 物资种类 | 食品 | 药品 | 生活用品 |
| 每辆汽车运载量(吨) | 6 | 5 | 4 |
| 每吨所需运费(元/吨) | 120 | 160 | 100 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
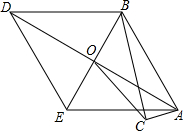 如图,在△ABC中,∠ACB=90°,AC=1,BC=2$\sqrt{3}$,以AB为边向左作菱形ABDE,使∠BAE=60°,AD,BE相交于点O,则CO的长是( )
如图,在△ABC中,∠ACB=90°,AC=1,BC=2$\sqrt{3}$,以AB为边向左作菱形ABDE,使∠BAE=60°,AD,BE相交于点O,则CO的长是( )| A. | $\frac{5}{2}$ | B. | 3 | C. | $\frac{9}{4}$ | D. | $\sqrt{6}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
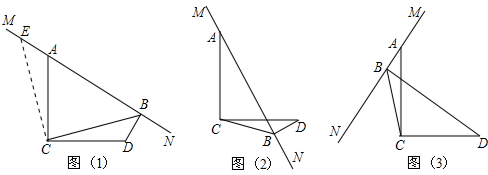
| 过点C作CE⊥CB于点C,与MN交于点E ∵∠ACB+∠BCD=90°,∠ACB+∠ACE=90°, ∴∠BCD=∠ACE. ∵四边形ACDB内角和为360°, ∴∠BDC+∠CAB=180°. ∵∠EAC+∠CAB=180°, ∴BD+AB=$\sqrt{2}$CB. | ∴∠EAC=∠BDC 又∵AC=DC, ∴△ACE≌△DCB, ∴AE=DB,CE=CB, ∴△ECB为等腰直角三角形, ∴BE=$\sqrt{2}$CB. 又∵BE=AE+AB, ∴BE=BD+AB. |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com