
【题目】如图,C为射线AB上一点,AB=30,AC比BC的 ![]() 多5,P,Q两点分别从A,B两点同时出发.分别以2单位/秒和1单位/秒的速度在射线AB上沿AB方向运动,运动时间为t秒,M为BP的中点,N为QM的中点,以下结论: ①BC=2AC;②AB=4NQ;③当PB=
多5,P,Q两点分别从A,B两点同时出发.分别以2单位/秒和1单位/秒的速度在射线AB上沿AB方向运动,运动时间为t秒,M为BP的中点,N为QM的中点,以下结论: ①BC=2AC;②AB=4NQ;③当PB= ![]() BQ时,t=12,其中正确结论的个数是( )
BQ时,t=12,其中正确结论的个数是( )![]()
A.0
B.1
C.2
D.3
【答案】C
【解析】解:设BC=x, ∴AC= ![]() x+5
x+5
∵AC+BC=AB
∴x+ ![]() x+5=30,
x+5=30,
解得:x=20,
∴BC=20,AC=10,
∴BC=2AC,故①成立,
∵AP=2t,BQ=t,
当0≤t≤15时,
此时点P在线段AB上,
∴BP=AB﹣AP=30﹣2t,
∵M是BP的中点
∴MB= ![]() BP=15﹣t
BP=15﹣t
∵QM=MB+BQ,
∴QM=15,
∵N为QM的中点,
∴NQ= ![]() QM=
QM= ![]() ,
,
∴AB=4NQ,
当15<t≤30时,
此时点P在线段AB外,且点P在Q的左侧,
∴AP=2t,BQ=t,
∴BP=AP﹣AB=2t﹣30,
∵M是BP的中点
∴BM= ![]() BP=t﹣15
BP=t﹣15
∵QM=BQ﹣BM=15,
∵N为QM的中点,
∴NQ= ![]() QM=
QM= ![]() ,
,
∴AB=4NQ,
当t>30时,
此时点P在Q的右侧,
∴AP=2t,BQ=t,
∴BP=AP﹣AB=2t﹣30,
∵M是BP的中点
∴BM= ![]() BP=t﹣15
BP=t﹣15
∵QM=BQ﹣BM=15,
∵N为QM的中点,
∴NQ= ![]() QM=
QM= ![]() ,
,
∴AB=4NQ,
综上所述,AB=4NQ,故②正确,
当0<t≤15,PB= ![]() BQ时,此时点P在线段AB上,
BQ时,此时点P在线段AB上,
∴AP=2t,BQ=t
∴PB=AB﹣AP=30﹣2t,
∴30﹣2t= ![]() t,
t,
∴t=12,
当15<t≤30,PB= ![]() BQ时,此时点P在线段AB外,且点P在Q的左侧,
BQ时,此时点P在线段AB外,且点P在Q的左侧,![]()
∴AP=2t,BQ=t,
∴PB=AP﹣AB=2t﹣30,
∴2t﹣30= ![]() t,
t,
t=20,
当t>30时,此时点P在Q的右侧,![]()
∴AP=2t,BQ=t,
∴PB=AP﹣AB=2t﹣30,
∴2t﹣30= ![]() t,
t,
t=20,不符合t>30,
综上所述,当PB= ![]() BQ时,t=12或20,故③错误;
BQ时,t=12或20,故③错误;
故选(C)
根据AC比BC的 ![]() 多5可分别求出AC与BC的长度,然后分别求出当P与Q重合时,此时t=30s,当P到达B时,此时t=15s,最后分情况讨论点P与Q的位置.
多5可分别求出AC与BC的长度,然后分别求出当P与Q重合时,此时t=30s,当P到达B时,此时t=15s,最后分情况讨论点P与Q的位置.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:
【题目】某电动自行车厂三月份的产量为1000辆,由于市场需求量不断增大,五月份的产量提高到1210辆,该厂四、五、六月份的月平均增长率相同,那么六月份的产量为__________辆.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小华骑自行车上学,当他骑了一段路时,想起要买本书,于是又这回到刚经过的某书店,买到书后继续去学校,以下是他本次上学所用的时间与离家距离的关系示意图.根据图中提供的信息回答下列问题: 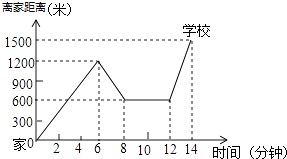
(1)小华家到学校的路程是m,小华在书店停留了min.
(2)在整个上学的途中哪个时间段小华的骑车速度最快?最快的速度是多少?
(3)本次上学途中,小华一共骑行了多少米?
(4)如果小华到校后立刻以300m/min的速度回家,请在原图上画出小华回家所用时间与离家距离的关系图象.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算下列各题
(1)计算:﹣12016+(﹣5)×[(﹣2)3+2]﹣(﹣4)2÷(﹣ ![]() )
)
(2)解方程:x﹣ ![]() =2﹣
=2﹣ ![]()
(3)已知:A= ![]() a﹣2(a﹣
a﹣2(a﹣ ![]() b2),B=﹣
b2),B=﹣ ![]() a+
a+ ![]() b2 , 且|a+2|+(b﹣3)2=0,求2A﹣6B的值.
b2 , 且|a+2|+(b﹣3)2=0,求2A﹣6B的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)﹣ ![]() ﹣21
﹣21 ![]() +3
+3 ![]() ﹣2
﹣2 ![]()
(2)﹣81÷2 ![]() ×
× ![]() ÷(﹣15)
÷(﹣15)
(3)+23× ![]() +(﹣57)×
+(﹣57)× ![]() +(﹣26)×
+(﹣26)× ![]()
(4)﹣14﹣[﹣2+(1﹣0.2÷ ![]() )×(﹣3)].
)×(﹣3)].
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,边长为1的正方形ABCD绕点A逆时针旋转45度后得到正方形AB′C′D′,边B′C′与DC交于点O,则四边形AB′OD的周长是( )

A.2![]()
B.3
C.![]()
D.1+![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com