
【题目】如图,在△ABC 中,点O是AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的角平分线于点E,交∠BCA的外角∠ACG平分线于点F.
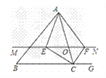
(1)试说明EO=FO;
(2)当点O运动到何处时,四边形AECF是矩形?并说明理由.
(3)当点O运动到何处,且△ABC满足什么条件时,四边形AECF 是正方形?并说明理由.
【答案】(1)证明见解析;(2) 当点O运动到AC的中点时,理由见解析;(3) 点O运动到AC的中点时,且△ABC满足∠ACB为直角的直角三角形时,理由见解析.
【解析】(1)由已知MN∥BC,CE、CF分别平分∠BCO和∠GCO,可推出∠OEC=∠OCE,∠OFC=∠OCF,所以得EO=CO=FO.
(2)由(1)得出的EO=CO=FO,点O运动到AC的中点时,则由EO=CO=FO=AO,所以这时四边形AECF是矩形.
(3)由已知和(2)得到的结论,点O运动到AC的中点时,且△ABC满足∠ACB为直角的直角三角形时,则推出四边形AECF是矩形且对角线垂直,所以四边形AECF是正方形.
解:(1)∵MN∥BC,
∴∠OEC=∠BCE,∠OFC=∠GCF,
又∵CE平分∠BCO,CF平分∠GCO,
∴∠OCE=∠BCE,∠OCF=∠GCF,
∴∠OCE=∠OEC,∠OCF=∠OFC,
∴EO=CO,FO=CO,
∴EO=FO.
(2)当点O运动到AC的中点时,四边形AECF是矩形.
∵当点O运动到AC的中点时,AO=CO,
又∵EO=FO,
∴四边形AECF是平行四边形,
∵FO=CO,
∴AO=CO=EO=FO,
∴AO+CO=EO+FO,即AC=EF,
∴四边形AECF是矩形.
(3)当点O运动到AC的中点时,且△ABC满足∠ACB为直角的直角三角形时,四边形AECF是正方形.
∵由(2)知,当点O运动到AC的中点时,四边形AECF是矩形,
已知MN∥BC,当∠ACB=90°,则
∠AOF=∠COE=∠COF=∠AOE=90°,
∴AC⊥EF,
∴四边形AECF是正方形.
“点睛”此题考查的知识点是正方形和矩形的判定及角平分线的定义,解题的关键是由已知得出EO=FO,然后根据(1)的结论确定(2)(3)的条件.


科目:初中数学 来源: 题型:
【题目】如图,把△OAB放置于平面直角坐标系xOy中,∠OAB=90°,OA=2,AB=![]() ,把△OAB沿x轴的负方向平移2OA的长度后得到△DCE.
,把△OAB沿x轴的负方向平移2OA的长度后得到△DCE.
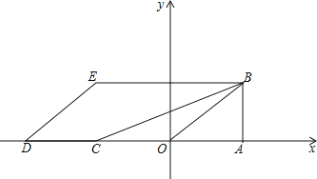
(1)若过原点的抛物线y=ax2+bx+c经过点B、E,求此抛物线的解析式;
(2)若点P在该抛物线上移动,当点p在第一象限内时,过点p作PQ⊥x轴于点Q,连接OP.若以O、P、Q为定点的三角形与以B、C、E为定点的三角形相似,直接写出点P的坐标;
(3)若点M(﹣4,n)在该抛物线上,平移抛物线,记平移后点M的对应点为M′,点B的对应点为B′.当抛物线向左或向右平移时,是否存在某个位置,使四边形M′B′CD的周长最短?若存在,求出此时抛物线的解析式;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】老师和小明同学玩数学游戏.老师取出一个不透明的口袋,口袋中装有三张分别标有数字1,2,3的卡片,卡片除数字外其余都相同,老师要求小明同学两次随机抽取一张卡片,并计算两次抽到卡片上的数字之积是奇数的概率.于是小明同学用画树状图的方法寻求他两次抽取卡片的所有可能结果.如图是小明同学所画的正确树状图的一部分.
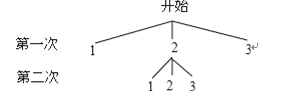
(1)补全小明同学所画的树状图;
(2)求小明同学两次抽到卡片上的数字之积是奇数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一元二次方程x2﹣8x﹣1=0配方后可变形为( )
A. (x+4)2=17 B. (x+4)2=15 C. (x﹣4)2=17 D. (x﹣4)2=15
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com