
【题目】如图,在菱形ABCD中,E、F分别是AB、BC边的中点,EP⊥CD于点P,∠BAD=110°,则∠FPC的度数是( )

A. 35° B. 45° C. 50° D. 55°
【答案】D
【解析】
延长PF、EB交于点G;连接EF,根据菱形的性质易证△BGF≌△CPF,根据全等三角形的性质可得PF=GF,即可得点F为PG的中点,又因∠GEP=90°,根据直角三角形斜边上的中线等于斜边的一半可得FP=FG=FE,所以∠FPC=∠FGB=∠GEF;连接AC,即可得∠GEF=∠BAC=![]() ∠BAD=55°,所以∠FPC的度数是55°.
∠BAD=55°,所以∠FPC的度数是55°.
延长PF、EB交于点G;连接EF,
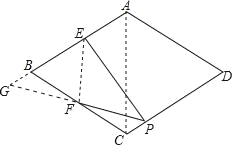
∵四边形ABCD是菱形,
∴AG∥DC,
∴∠GBF=∠PCF,
∵F是BC中点,
∴BF=CF,
在△BGF和△CPF中, ,
,
∴△BGF≌△CPF,
∴PF=GF,
∴点F为PG的中点,
∵∠GEP=90°,
∴FP=FG=FE,
∴∠FPC=∠FGB=∠GEF,
连接AC,
则∠GEF=∠BAC=![]() ∠BAD=55°,
∠BAD=55°,
∴∠FPC的度数是55°.
故选D.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在矩形纸片ABCD中,点P在边AB上,沿着PC折叠纸片使B点落在边AD上的E点处,过点E作EF∥AB交PC于F,连接BF.
(1)求证:四边形BFEP为菱形;
(2)若tan∠BCP=![]() ,AB=3cm,求AE的长.
,AB=3cm,求AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 的图象如图所示,它与
的图象如图所示,它与![]() 轴的两个交点分别为
轴的两个交点分别为![]() ,
,![]() .对于下列命题:①
.对于下列命题:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中正确的有( )
.其中正确的有( )

A. ![]() 个 B.
个 B. ![]() 个 C.
个 C. ![]() 个 D.
个 D. ![]() 个
个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在菱形ABCD中,记∠ABC=∠α(0°<∠α<90°),菱形的面积记作S,菱形的周长记作C,若AD=2,则( )
A. C与∠α的大小有关
B. 当∠α=45°时,S=![]()
C. A,B,C,D四个点可以在同一个圆上
D. S随∠α的增大而增大
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD的边长为![]() ,连接AC、BD交于点O,CE平分∠ACD交BD于点E,
,连接AC、BD交于点O,CE平分∠ACD交BD于点E,
(1)求DE的长;
(2)过点EF作EF⊥CE,交AB于点F,求BF的长;
(3)过点E作EG⊥CE,交CD于点G,求DG的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC中,∠CAB=90°,AC=AB=3,△CDE中,∠CDE=90°,CD=DE=5,连接BE,取BE中点F,连接AF、DF.

(1)如图1,若C、B、E三点共线,H为BC中点.
①直接指出AF与DF的关系 ;
②直接指出FH的长度 ;
(2)将图(1)中的△CDE绕C点逆时针旋转a(如图2,0°<α<180°),试确定AF与DF的关系,并说明理由;
(3)在(2)中,若AF=![]() ,请直接指出点F所经历的路径长.
,请直接指出点F所经历的路径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是某市2009年4月5日至14日每天最低气温的折线统计图.
(1)图2是该市2007年4月5日至14日每天最低气温的频数分布直方图,根据图1提供的信息,补全图2中频数分布直方图;
(2)在这10天中,最低气温的众数是____,中位数是____,方差是_____.
(3)请用扇形图表示出这十天里温度的分布情况.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ABC和△ADE中,AB=AC,AD=AE,且∠BAC=∠DAE.
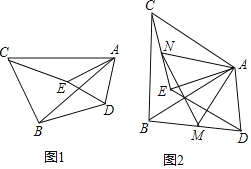
(1)求证:BD=CE;
(2)若点M,N分别是BD,CE的中点,如图2,连接AM,AN,MN,若AC=6,AE=4,∠EAC=60°,求AN的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com