
 (2012•合山市模拟)矩形OABC在平面直角坐标系中的位置如图所示,其中OA=5,AB=2,抛物线y=-x2+3x的图象与BC交于D、E两点.
(2012•合山市模拟)矩形OABC在平面直角坐标系中的位置如图所示,其中OA=5,AB=2,抛物线y=-x2+3x的图象与BC交于D、E两点.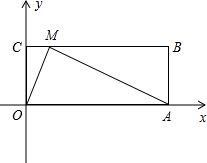 (2)如右图;
(2)如右图;| CM |
| AB |
| OC |
| BM |
| m |
| 2 |
| 2 |
| 5-m |
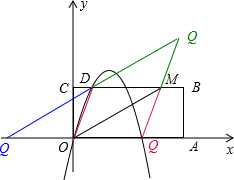 (3)若以D、O、Q、M为顶点的四边形是平行四边形,那么点D、M不共点,所以点M取(4,2);
(3)若以D、O、Q、M为顶点的四边形是平行四边形,那么点D、M不共点,所以点M取(4,2);

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com