
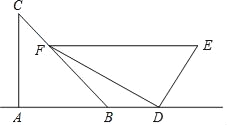
【题目】小华是一位善于思考的学生,在一次数学活动课上,他将一副直角三角板如图位置摆放,A,B,D在同一直线上,EF∥AD,∠CAB=∠EDF=90°,∠C=45°,∠E=60°,量得DE=2![]() .则BD=_____.
.则BD=_____.
 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:初中数学 来源: 题型:
【题目】端午节放假期间,小明和小华准备到宜宾的蜀南竹海(记为A)、兴文石海(记为B)、夕佳山居民(记为C)、李庄古镇(记为D)中的一个景点去游玩,他们各自在这四个景点中任选一个,每个景点被选中的可能性相同.
(1)小明选择去蜀南竹海旅游的概率为________;
(2)用画树状图或列表的方法求小明和小华都选择去兴文石海旅游的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2017浙江省嘉兴市,第20题,8分)如图,一次函数![]() (
(![]() )与反比例函数
)与反比例函数![]() (
(![]() )的图象交于点A(﹣1,2),B(m,﹣1).
)的图象交于点A(﹣1,2),B(m,﹣1).
(1)求这两个函数的表达式;
(2)在x轴上是否存在点P(n,0)(n>0),使△ABP为等腰三角形?若存在,求n的值;若不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C是线段AB上除点A、B外的任意一点,分别以AC、BC为边在线段AB的同旁作等边△ACD和等边△BCE,连接AE交DC于M,连接BD交CE于N,连接MN.
(1)求证:AE=BD;
(2)请判断△CMN的形状,并说明理由。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的周长为32,点D、E都在边BC上,∠ABC的平分线垂直于AE,垂足为Q,∠ACB的平分线垂直于AD,垂足为P,若BC=12,则PQ的长为( )
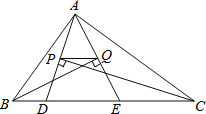
A.3B.4C.5D.6
查看答案和解析>>
科目:初中数学 来源: 题型:
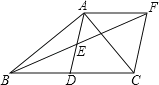
【题目】如图,在△ABC中,∠BAC=90°,AD是中线,E是AD的中点,过点A作AF∥BC交BE的延长线于点F,连接CF
(1)求证:AD=CF;
(2)如果AB=AC,四边形ADCF的形状为 (直接写出结果);
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形OABC的顶点O是坐标原点,边OA和OC分别在x轴、y轴上,点B的坐标为(4,4).直线l经过点C.
(1)若直线l与边OA交于点M,过点A作直线l的垂线,垂足为D,交y轴于点E.
①如图1,当OE=1时,求直线l对应的函数表达式;
②如图2,连接OD,求证:OD平分∠CDE.
(2)如图3,若直线l与边AB交于点P,且S△BCP=![]() S四边形AOCP,此时,在x轴上是否存在点Q,使△CPQ是以CP为直角边的直角三角形?若存在,求点Q的坐标,若不存在,请说明理由.
S四边形AOCP,此时,在x轴上是否存在点Q,使△CPQ是以CP为直角边的直角三角形?若存在,求点Q的坐标,若不存在,请说明理由.
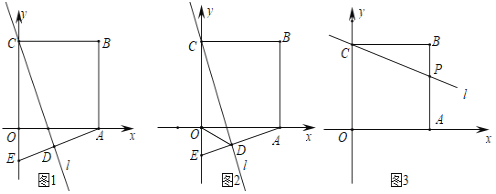
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在Rt△ABC中,∠C=90°,AC=BC=2,点D、E分别在边AC、AB上,AD=DE=![]() AB,连接DE.将△ADE绕点A逆时针方向旋转,记旋转角为θ.
AB,连接DE.将△ADE绕点A逆时针方向旋转,记旋转角为θ.
(1)问题发现
①当θ=0°时,![]() = ;
= ;
②当θ=180°时,![]() = .
= .
(2)拓展探究
试判断:当0°≤θ<360°时,![]() 的大小有无变化?请仅就图2的情形给出证明;
的大小有无变化?请仅就图2的情形给出证明;
(3)问题解决
①在旋转过程中,BE的最大值为 ;
②当△ADE旋转至B、D、E三点共线时,线段CD的长为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是规格为![]() 的正方形网格,请在所给网格中按下列要求操作:
的正方形网格,请在所给网格中按下列要求操作:
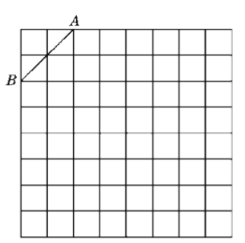
(1)请在网格中建立平面直角坐标系,使点A的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ;
;
(2)在第二象限内的格点上找一点![]() ,使点
,使点![]() 与线段
与线段![]() 组成一个以
组成一个以![]() 为底的等腰三角形,且腰长是无理数,画出
为底的等腰三角形,且腰长是无理数,画出![]() ,则点
,则点![]() 的坐标是 ,
的坐标是 ,![]() 的周长是 (结果保留根号);
的周长是 (结果保留根号);
(3)作出![]() 关于
关于![]() 轴对称的
轴对称的![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com