
【题目】在平面直角坐标系xOy中,点M的坐标为(x1,y1),点N的坐标为(x2,y2),且x1≠x2,y1≠y2,以MN为边构造菱形,若该菱形的两条对角线分别平行于x轴,y轴,则称该菱形为边的“坐标菱形”.
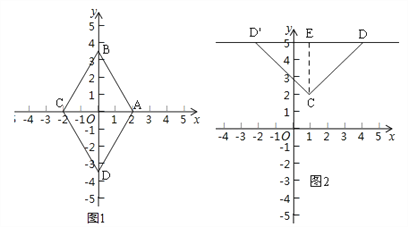
(1)已知点A(2,0),B(0,2![]() ),则以AB为边的“坐标菱形”的最小内角为 ;
),则以AB为边的“坐标菱形”的最小内角为 ;
(2)若点C(1,2),点D在直线y=5上,以CD为边的“坐标菱形”为正方形,求直线CD 表达式;
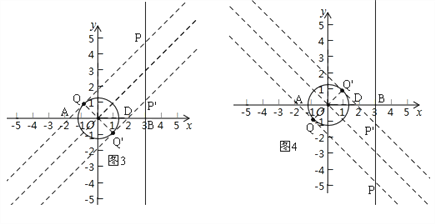
(3)⊙O的半径为![]() ,点P的坐标为(3,m).若在⊙O上存在一点Q,使得以QP为边的“坐标菱形”为正方形,求m的取值范围.
,点P的坐标为(3,m).若在⊙O上存在一点Q,使得以QP为边的“坐标菱形”为正方形,求m的取值范围.
【答案】(1)60°;(2)y=x+1或y=﹣x+3;(3)1≤m≤5或﹣5≤m≤﹣1
【解析】分析:(1)根据定义建立以AB为边的“坐标菱形”,由勾股定理求边长AB=4,可得30度角,从而得最小内角为60°;
(2)先确定直线CD与直线y=5的夹角是45°,得D(4,5)或(﹣2,5),易得直线CD的表达式为:y=x+1或y=﹣x+3;
(3)分两种情况:
①先作直线y=x,再作圆的两条切线,且平行于直线y=x,如图3,根据等腰直角三角形的性质分别求P'B=BD=1,PB=5,写出对应P的坐标;
②先作直线y=﹣x,再作圆的两条切线,且平行于直线y=﹣x,如图4,同理可得结论.
详解:(1)∵点A(2,0),B(0,2![]() ),∴OA=2,OB=2
),∴OA=2,OB=2![]() .在Rt△AOB中,由勾股定理得:AB=
.在Rt△AOB中,由勾股定理得:AB=![]() =4,∴∠ABO=30°.
=4,∴∠ABO=30°.
∵四边形ABCD是菱形,∴∠ABC=2∠ABO=60°.
∵AB∥CD,∴∠DCB=180°﹣60°=120°,∴以AB为边的“坐标菱形”的最小内角为60°.
故答案为:60°;
(2)如图2.
∵以CD为边的“坐标菱形”为正方形,∴直线CD与直线y=5的夹角是45°.
过点C作CE⊥DE于E,∴D(4,5)或(﹣2,5),∴直线CD的表达式为:y=x+1或y=﹣x+3;
(3)分两种情况:
①先作直线y=x,再作圆的两条切线,且平行于直线y=x,如图3.
∵⊙O的半径为![]() ,且△OQ'D是等腰直角三角形,∴OD=
,且△OQ'D是等腰直角三角形,∴OD=![]() OQ'=2,∴P'D=3﹣2=1.
OQ'=2,∴P'D=3﹣2=1.
∵△P'DB是等腰直角三角形,∴P'B=BD=1,∴P'(0,1),同理可得:OA=2,∴AB=3+2=5.
∵△ABP是等腰直角三角形,∴PB=5,∴P(0,5),∴当1≤m≤5时,以QP为边的“坐标菱形”为正方形;
②先作直线y=﹣x,再作圆的两条切线,且平行于直线y=﹣x,如图4.
∵⊙O的半径为![]() ,且△OQ'D是等腰直角三角形,∴OD=
,且△OQ'D是等腰直角三角形,∴OD=![]() OQ'=2,∴BD=3﹣2=1.
OQ'=2,∴BD=3﹣2=1.
∵△P'DB是等腰直角三角形,∴P'B=BD=1,∴P'(0,﹣1),同理可得:OA=2,∴AB=3+2=5.
∵△ABP是等腰直角三角形,∴PB=5,∴P(0,﹣5),∴当﹣5≤m≤﹣1时,以QP为边的“坐标菱形”为正方形;
综上所述:m的取值范围是1≤m≤5或﹣5≤m≤﹣1.


科目:初中数学 来源: 题型:
【题目】疫情无情人有情,爱心捐款传真情,新型冠状病毒感染的肺炎疫情期间,某班学生积极参加献爱心活动,该班50名学生的捐款统计情况如下表:
金额/元 | 5 | 10 | 20 | 50 | 100 |
人数 | 6 | 17 | 14 | 8 | 5 |
则他们捐款金额的众数和中位数分别是( )
A.100,10B.10,20C.17,10D.17,20
查看答案和解析>>
科目:初中数学 来源: 题型:
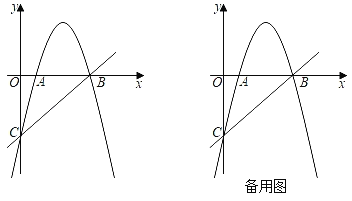
【题目】如图,抛物线y=ax2+6x+c交x轴于A,B两点,交y轴于点C.直线y=x﹣5经过点B,C.
(1)求抛物线的解析式;
(2)若点N为抛物线上动点,当∠NBA=∠OAC时,求点N的坐标,
(3)过点A的直线交直线BC于点M,当AM⊥BC时,过抛物线上一动点P(不与点B,C重合),作直线AM的平行线交直线BC于点Q,若以点A,M,Q,P为顶点的四边形是平行四边形,求点P的横坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为响应“把中国人的饭碗牢牢端在自己手中”的号召,确保粮食安全,优选品种,提高产量,某农业科技小组对A、B两个玉米品种进行实验种植对比研究.去年A、B两个品种各种植了10亩.收获后A、B两个品种的售价均为2.4元/kg,且B品种的平均亩产量比A品种高100千克,A、B两个品种全部售出后总收入为21600元.
(1)求A、B两个品种去年平均亩产量分别是多少千克?
(2)今年,科技小组优化了玉米的种植方法,在保持去年种植面积不变的情况下,预计A、B两个品种平均亩产量将在去年的基础上分别增加a%和2a%.由于B品种深受市场欢迎,预计每千克售价将在去年的基础上上涨a%,而A品种的售价保持不变,A、B两个品种全部售出后总收人将增加![]() ,求a的值.
,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某家具商场计划购进某种餐桌、餐椅进行销售,有关信息如下表:
原进价(元/张) | 零售价(元/张) | 成套售价(元/套) | |
餐桌 | a | 380 | 940 |
餐椅 |
| 160 |
已知用600元购进的餐椅数量与用1300元购进的餐桌数量相同.
(1)求表中a的值;
(2)该商场计划购进餐椅的数量是餐桌数量的5倍还多20张,且餐桌和餐椅的总数量不超过200张.若将一半的餐桌成套(一张餐桌和四张餐椅配成一套)销售,其余餐桌、餐椅以零售方式销售,请问怎样进货,才能获得最大利润?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有![]() 、
、![]() 两组卡片,卡片上除数字外完全相同,
两组卡片,卡片上除数字外完全相同,![]() 组有三张,分别标有数字
组有三张,分别标有数字![]() 、
、![]() 、
、![]() .
.![]() 组有二张,分别标有数字
组有二张,分别标有数字![]() 、
、![]() .小明闭眼从
.小明闭眼从![]() 组中随机抽出一张,记录其标有的数字为
组中随机抽出一张,记录其标有的数字为![]() ,再从
,再从![]() 组中随机抽出一张,记录其标有的数字为
组中随机抽出一张,记录其标有的数字为![]() ,这样就确定点
,这样就确定点![]() 的一个坐标为
的一个坐标为![]() .
.
(1)用列表或画树状图的方法写出点![]() 的所有可能坐标;
的所有可能坐标;
(2)求点![]() 落在第一象限的概率.
落在第一象限的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
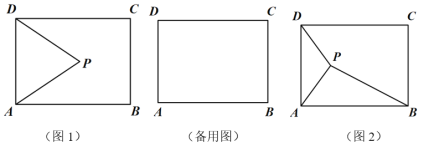
【题目】(阅读理解)设点P在矩形ABCD内部,当点P到矩形的一条边的两个端点距离相等时,称点P为该边的“和谐点”.例如:如图1,矩形ABCD中,若PA=PD,则称P为边AD的“和谐点”.
(解题运用)已知,点P在矩形ABCD内部,且AB=10,BC=6.
(1)设P是边AD的“和谐点”,则P 边BC的“和谐点”(填“是”或“不是”);
(2)若P是边BC的“和谐点”,连接PA,PB,当△PAB是直角三角形时,求PA的值;
(3)如图2,若P是边AD的“和谐点”,连接PA,PB,PD,求tan∠PAB· tan∠PBA的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】古希腊著名的毕达哥拉斯学派把1、3、6、10、……这样的数称为“三角形数”,而把1、4、16、……这样的数称为“正方形数”.从图中可以发现,任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和.按下列图示中的规律,请写出第9个等式_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,直线y=﹣![]() x与反比例函数y=
x与反比例函数y=![]() 的图象交于关于原点对称的A,B两点,已知A点的纵坐标是3.
的图象交于关于原点对称的A,B两点,已知A点的纵坐标是3.
(1)求反比例函数的表达式;
(2)将直线y=﹣![]() x向上平移后与反比例函数在第二象限内交于点C,如果△ABC的面积为48,求平移后的直线的函数表达式.
x向上平移后与反比例函数在第二象限内交于点C,如果△ABC的面积为48,求平移后的直线的函数表达式.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com