
 ���Σ������ڣ���������з��������ĵ�P�����ꣻ�������ڣ���˵�����ɣ�
���Σ������ڣ���������з��������ĵ�P�����ꣻ�������ڣ���˵�����ɣ� ��
�� ����
����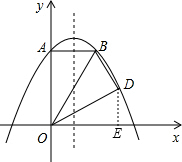 �⣺��1������D��DE��x���ڵ�E����ͼ��1����
�⣺��1������D��DE��x���ڵ�E����ͼ��1����

 ��
�� ��
�� =
= ��
�� ��3����
��3���� ��3����D��
��3����D�� ��
�� �����㣬
�����㣬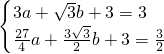

 x2+
x2+ x+3��
x+3��
 x2+
x2+ x+3�Ķ��㣬
x+3�Ķ��㣬 ��
�� ����
���� ��3�����룬��k=
��3�����룬��k= ��
�� x��
x�� x����F��
x����F�� ��
�� ����
���� ��G��x��
��G��x�� ����
���� x2+
x2+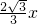 +3����
+3���� x-
x- =
= -��-
-��- x2+
x2+ x+3����
x+3���� x2+
x2+ x+3+
x+3+ x=5��
x=5�� ��x2=
��x2= ��
�� ��6����P2��������
��6����P2�������� ��
�� ����F�غϣ�Ӧ��ȥ��
����F�غϣ�Ӧ��ȥ�� ��6����
��6����

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
 22����ͼ����֪Rt��ABC��AB=AC����ABC��ƽ����BD��AC�ڵ�D��BD�Ĵ�ֱƽ���߷ֱ�AB��BC�ڵ�E��F��CD=CG��
22����ͼ����֪Rt��ABC��AB=AC����ABC��ƽ����BD��AC�ڵ�D��BD�Ĵ�ֱƽ���߷ֱ�AB��BC�ڵ�E��F��CD=CG���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
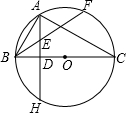 E������O�ڵ�F����AE=BE��
E������O�ڵ�F����AE=BE�� |
| AB |
 |
| AF |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 5����ͼ����֪Rt��ABC�У���BAC=90�㣬AB=AC��P��BC�ӳ�����һ�㣬PE��AB��BA�ӳ�����E��PF��AC��AC�ӳ�����F��DΪBC�е㣬����DE��DF����֤��DE=DF��
5����ͼ����֪Rt��ABC�У���BAC=90�㣬AB=AC��P��BC�ӳ�����һ�㣬PE��AB��BA�ӳ�����E��PF��AC��AC�ӳ�����F��DΪBC�е㣬����DE��DF����֤��DE=DF���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��ͼ����֪Rt��ABC�У���CAB=30�㣬BC=5������A��AE��AB����AE=15������BE��AC�ڵ�P��
��ͼ����֪Rt��ABC�У���CAB=30�㣬BC=5������A��AE��AB����AE=15������BE��AC�ڵ�P���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��ͼ����֪Rt��ABC�С�A=90�㣬AB=3��AC=4�������ر�AB����ƽ��2����λ�õ���FGE�����ı���ACEG�����Ϊ
��ͼ����֪Rt��ABC�С�A=90�㣬AB=3��AC=4�������ر�AB����ƽ��2����λ�õ���FGE�����ı���ACEG�����Ϊ�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com