
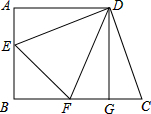
 如图,正方形ABCD中,边长为12,DE⊥DC交AB于点E,DF平分∠EDC交BC于点F,连接EF.
如图,正方形ABCD中,边长为12,DE⊥DC交AB于点E,DF平分∠EDC交BC于点F,连接EF.分析 (1)根据正方形的性质和全等三角形的判定和性质证明即可;
(2)设EF=x,根据勾股定理解答即可.
解答 (1)证明:∵正方形ABGD,
又∵DE⊥DC,
∴∠ADE+∠EDG=90°=∠GDC+∠EDG,
∴∠ADE=∠GDC.
又∵∠A=∠DGC,
且AD=GD,
在△ADE与△GDC中,
$\left\{\begin{array}{l}{∠ADE=∠GDC}\\{AD=DG}\\{∠A=∠DGC}\end{array}\right.$,
∴△ADE≌△GDC(ASA).
∴DE=DC,且AE=GC.
在△EDF和△CDF中,
$\left\{\begin{array}{l}{DE=DC}\\{∠EDF=∠D=CDF}\\{DF=DF}\end{array}\right.$,
∴△EDF≌△CDF(SAS).
∴EF=CF;
(2)解:∵$\frac{AE}{AD}$=$\frac{1}{3}$,
∴AE=GC=4.
设EF=x,则BF=16-CF=16-x,BE=12-4=8.
由勾股定理,得x2=(16-x)2+82.
解之,得x=10,
即EF=10.
点评 此题考查正方形的性质,关键是根据正方形的性质和全等三角形的判定和性质解答.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
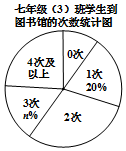 为了落实漳州市教育局关于全市中小学生每天阅读1小时的文件精神.某校对七年级(3)班全体学生一周到图书馆的次数做了调查统计,以下是调查过程中绘制的还不完整的两个统计图.请你根据统计图表中的信息,解答下列问题:
为了落实漳州市教育局关于全市中小学生每天阅读1小时的文件精神.某校对七年级(3)班全体学生一周到图书馆的次数做了调查统计,以下是调查过程中绘制的还不完整的两个统计图.请你根据统计图表中的信息,解答下列问题:| 到图书馆的 次数 | 0次 | 1次 | 2次 | 3次 | 4次及 以上 |
| 人数 | 5 | 10 | m | 8 | 12 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
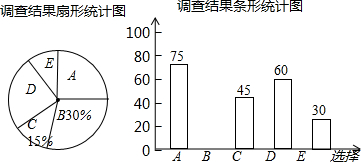
| 造成医患关系紧张的原因(单选) A.药价高 B.检测项目太多且收费太高 C.住院报销比例低 D.医疗费与个人收入不相称 E.其他 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在平面直角坐标系xOy,直线y=x-1与y轴交于点A,与双曲线y=$\frac{k}{x}$交于点B(m,2)
在平面直角坐标系xOy,直线y=x-1与y轴交于点A,与双曲线y=$\frac{k}{x}$交于点B(m,2)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com