
 如图,分别表示甲步行与乙骑自行车(在同一条路上)行走的路程S甲、S乙与时间t的关系,观察图象并回答下列问题:
如图,分别表示甲步行与乙骑自行车(在同一条路上)行走的路程S甲、S乙与时间t的关系,观察图象并回答下列问题:分析 (1)根据t=0时甲乙两人的路程差即为两人的距离解答;
(2)根据s不变的时间即为修车时间解答;
(3)根据两人的函数图象的交点即为相遇写出时间即可;
(4)利用速度与时间路程的关系解答;
(5)利用速度与时间路程的关系解答.
解答 解::(1)乙出发时,与甲相距10千米;
(2)走了一段路程后,乙的自行车发生故障,停下来修理,修车的时间为1.5-0.5=1小时;
(3)乙从出发起,经过3小时与甲相遇;
(4)甲行走的平均速度是$\frac{22.5-10}{3}=\frac{25}{6}$千米/小时;
(5)$\frac{7.5}{0.5}=15$,$\frac{22.5-7.5}{3-1.5}=10$,乙骑自行车出故障前的速度与修车后的速度不一样.
故答案为:10;1;3;$\frac{25}{6}$.
点评 本题考查了一次函数的应用,主要利用了待定系数法求一次函数解析式,时间、路程、速度三者之间的关系,准确识图是解题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
 清明小长假的第二天上午8时,小张自驾小汽车从家出发,带全家人去离家200千米的一个4A级景区游玩,小张驾驶的小汽车离家的距离y(千米)与时间t(时)之间的关系如图所示,请结合图象解决下列问题:
清明小长假的第二天上午8时,小张自驾小汽车从家出发,带全家人去离家200千米的一个4A级景区游玩,小张驾驶的小汽车离家的距离y(千米)与时间t(时)之间的关系如图所示,请结合图象解决下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在滨湖新区一笔直的公路l上有A,B两个学校,A在B的正东方向,学校A的北偏西60°方向2千米的P处,有一正在建设的地铁站口,从B学校测得地铁站口P在它的北偏东45°方向.求学校B离地铁站的距离(即BP的长)和A,B两个学校间的距离(结果都保留根号).
在滨湖新区一笔直的公路l上有A,B两个学校,A在B的正东方向,学校A的北偏西60°方向2千米的P处,有一正在建设的地铁站口,从B学校测得地铁站口P在它的北偏东45°方向.求学校B离地铁站的距离(即BP的长)和A,B两个学校间的距离(结果都保留根号).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
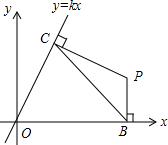 如图,在平面直角坐标系中,直线y=kx(k≠0)经过点(a,$\sqrt{3}$a)(a>0),线段BC的两个端点分别在x轴与直线y=kx上(点B、C均与原点O不重合)滑动,且BC=2,分别作BP⊥x轴,CP⊥直线y=kx,交点为P.经探究,在整个滑动过程中,P、O两点间的距离为定值$\frac{4}{3}\sqrt{3}$.
如图,在平面直角坐标系中,直线y=kx(k≠0)经过点(a,$\sqrt{3}$a)(a>0),线段BC的两个端点分别在x轴与直线y=kx上(点B、C均与原点O不重合)滑动,且BC=2,分别作BP⊥x轴,CP⊥直线y=kx,交点为P.经探究,在整个滑动过程中,P、O两点间的距离为定值$\frac{4}{3}\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在平面直角坐标系中,直线 y=-2x+1与 y轴交于点 C,直线 y=x+k( k≠0)与 y轴交于点 A,与直线 y=-2x+1交于点 B,设点 B的横坐标为-2.
在平面直角坐标系中,直线 y=-2x+1与 y轴交于点 C,直线 y=x+k( k≠0)与 y轴交于点 A,与直线 y=-2x+1交于点 B,设点 B的横坐标为-2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com