13．问题提出：求边长分别为$\sqrt{4+{a}^{2}}$，$\sqrt{1+9{a}^{2}}$，$\sqrt{9+4{a}^{2}}$（a为正整数）三角形的面积．
问题探究：为解决上述数学问题，我们采取数形结合和转化的思想方法，并采取一般问题特殊化的策略来进行探究．
探究一：当a=1时，求边长分别为$\sqrt{5}$、$\sqrt{10}$、$\sqrt{13}$三角形的面积．
先画一个正方形网格（每个小正方形的边长为1），再在网格中画出边长分别为$\sqrt{5}$，$\sqrt{10}$，$\sqrt{13}$的格点三角形△ABC（如图①）．
因为AB是直角边分别为2和1的Rt△ABE的斜边，所以AB=$\sqrt{5}$；
因为BC是直角边分别为1和3的Rt△BCF的斜边，所以BC=$\sqrt{10}$；
因为AC是直角边分别为3和2的Rt△ACG的斜边，所以AC=$\sqrt{13}$；通过面积转化，可间接求三角形△ABC的面积．
所以，S
△ABC=S
正方形EFCG-S
△ABE-S
△BCF-S
△ACG．
（1）直接写出图①中S
△ABC=3.5．
探究二：当a=2时，求边长分别为2$\sqrt{2}$，$\sqrt{37}$，5三角形的面积．
先画一个长方形网格（每个小长方形的长为2，宽为1），再在网格中画出边长分别为2$\sqrt{2}$，$\sqrt{37}$，5的格点三角形△ABC（如图②）．
因为AB是直角边分别为2和2的Rt△ABE的斜边，所以AB=2$\sqrt{2}$；
因为BC是直角边分别为1和6的Rt△BCF的斜边，所以BC=$\sqrt{37}$；
因为AC是直角边分别为3和4的Rt△ACG的斜边，所以AC=5，通过面积转化，可间接求三角形△ABC的面积．
所以，S
△ABC=S
正方形EFCG-S
△ABE-S
△BCF-S
△ACG（2）直接写出图②中S
△ABC=7．
探究三：当a=3时，求边长分别为$\sqrt{13}$，$\sqrt{82}$，3$\sqrt{5}$三角形的面积．
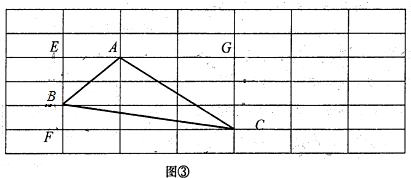
仿照上述方法解答下列问题：
（3）画的长方形网格中，每个小长方形的长应是2．
（4）边长分别为$\sqrt{13}$，$\sqrt{82}$，3$\sqrt{5}$的三角形的面积为$\frac{21}{2}$．
问题解决：求边长分别为$\sqrt{4+{a}^{2}}$，$\sqrt{1+9{a}^{2}}$，$\sqrt{9+4{a}^{2}}$（a为正整数）三角形的面积．
（5）类比上述方法画长方形网格，每个小长方形的长应是a．
（6）边长分别为$\sqrt{4+{a}^{2}}$，$\sqrt{1+9{a}^{2}}$，$\sqrt{9+4{a}^{2}}$（a为正整数）的三角形的面积是$\frac{7}{2}$a．
如图，矩形ABCD中，AB=8，BC=6，P为AD上一点，将△ABP沿BP翻折至△EBP，PE与CD相交于点O，且OE=OD．
如图，两个全等的等边三角形△ABC，△DEF的一边重叠地放在直线l上，AC、DE交于点P．
