
【题目】如图,已知∠1=∠2,∠B=∠C,试证明AB∥CD. 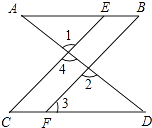
【答案】解:∵∠1=∠2(已知),且∠1=∠4(对顶角相等),
∴∠2=∠4 (等量代换),
∴CE∥BF (同位角相等,两直线平行),
∴∠C=∠3(两直线平行,同位角相等);
又∵∠B=∠C(已知),
∴∠3=∠B(等量代换),
∴AB∥CD (内错角相等,两直线平行)
【解析】首先证明CE∥BF,得到∠C=∠3,从而证得∠3=∠B,根据内错角相等,两直线平行即可证得.
【考点精析】本题主要考查了平行线的判定与性质的相关知识点,需要掌握由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】某市现有42万人口,计划一年后城镇人口增加0.8%,农村人口增加1.1%,这样全市人口将增加1%,求这个市现在的城镇人口与农村人口?
设城镇人口是x万,农村人口是y万,根据题意填写下表,并列出方程组求x、y的值.
城镇 | 农村 | 全市 | |
现有人数(万人) | x | y | 42 |
一年后增加人口(万人) |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图形的操作过程:
在图①中,将线段A1A2向右平移1个单位到B1B2 , 得到封闭图形A1A2B2B1(即阴影部分);
在图②中,将折线A1A2A3向右平移1个单位到B1B2B3 , 得到封闭图形A1A2A3B3B2B1(即阴影部分).
(1)在图③中,请你类似地画一条有两个折点的折线,同样向右平移1个单位,从而得到一个封闭图形,并用斜线画出阴影; 
(2)请你分别写出上述三个图形中除去阴影部分后剩余部分的面积:
S1= , S2= , S3= .
(3)联想与探索:
如图④在一块矩形草地上,有一条弯曲的柏油小路(小路任何地方的水平宽度都是1个单位),请你猜想空白部分表示的草地面积是多少并说明你的猜想是正确的.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),AB∥CD,猜想∠BPD与∠B,∠D的关系,说出理由.
解:猜想∠BPD+∠B+∠D=360°
理由:过点P作EF∥AB,
∴∠B+∠BPE=180°(两直线平行,同旁内角互补)
∵AB∥CD,EF∥AB,
∴EF∥CD,(如果两条直线都和第三条直线平行,那么这两条直线也互相平行.)
∴∠EPD+∠D=180°(两直线平行,同旁内角互补)
∴∠B+∠BPE+∠EPD+∠D=360°
∴∠B+∠BPD+∠D=360°
(1)依照上面的解题方法,观察图(2),已知AB∥CD,猜想图中的∠BPD与∠B,∠D的关系,并说明理由.
(2)观察图(3)和(4),已知AB∥CD,猜想图中的∠BPD与∠B,∠D的关系,不需要说明理由. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图①,在平行四边形ABCD中,AB=3cm,BC=5cm,AC⊥AB.△ACD沿AC的方向匀速平移得到△PNM,速度为1cm/s;同时,点Q从点C出发,沿着CB方向匀速移动,速度为1cm/s;当△PNM停止平移时,点Q也停止移动,如图②.设移动时间为t(s)(0<t<4).连接PQ、MQ、MC.解答下列问题:

(1)当t为何值时,PQ∥AB?
(2)当t=3时,求△QMC的面积;
(3)是否存在某一时刻t,使PQ⊥MQ?若存在,求出t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,无限循环小数都可以转化为分数.例如:将 ![]() 转化为分数时,可设
转化为分数时,可设 ![]() =x,则x=0.3+
=x,则x=0.3+ ![]() x,解得x=
x,解得x= ![]() ,即
,即 ![]() =
= ![]() .仿此方法,将
.仿此方法,将 ![]() 化成分数是 .
化成分数是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com