
ЁОЬтФПЁПЖЈвхЃКСЌНгХзЮяЯпЩЯСНЕуЕФЯпЖЮНаХзЮяЯпЕФЯвЃЌдкетСНЕужЎМфХзЮяЯпЩЯЕФШЮвтвЛЕуPгыДЫСНЕуЙЙГЩЕФШ§НЧаЮГЦзїХзЮяЯпЕФЯвШ§НЧЃЌЕуPГЦзїЯвзЖЃЌЩшЕуPЕФКсзјБъЮЊxЃЎ
вбжЊХзЮяЯпОЙ§AЃЈ1ЃЌ2ЃЉЁЂBЃЈmЃЌnЃЉЁЂCЃЈ3ЃЌЉ2ЃЉШ§ЕуЃЌPЪЧХзЮяЯпЩЯACжЎМфЕФвЛЕуЃЌвдACЮЊЯвЕФЯвШ§НЧЮЊЁїPAC.
ЃЈ1ЃЉЭМвЛЃЌЕБmЃН2ЃЌnЃН1ЪБЃЌЧѓИУХзЮяЯпЕФНтЮіЪНЃЌШєxЃНk1ЪБЁїPACЕФУцЛ§зюДѓЃЌЧѓk1ЕФжЕЃЎ
ЃЈ2ЃЉЭМЖўЃЌЕБmЃН2ЃЌnЁй1ЪБЃЌгУnБэЪОИУХзЮяЯпЕФНтЮіЪНЃЌШєxЃНk2ЪБЁїPACЕФУцЛ§зюДѓЃЌЧѓk2ЕФжЕЃЎk1гыk2гаКЮЪ§СПЙиЯЕЃП
ЃЈ3ЃЉЭМШ§ЃЌЕБmЁй2ЃЌnЁй1ЪБЃЌгУmЃЌnБэЪОИУХзЮяЯпЕФНтЮіЪНЃЌШєxЃНk3ЪБЁїPACЕФУцЛ§зюДѓЃЌЧѓk3ЕФжЕЃЎЙлВьЭМ1ЃЌ2ЃЌ3ЃЌЙ§ЖЈЕуAЁЂCЃЌИљОнBдкИїжжВЛЭЌЮЛжУЫљЕУМЦЫуНсЙћЃЌФуЗЂЯжЭЈЙ§СНИіЖЈЕуЕФХзЮяЯпЯЕжаЃЌвдДЫСНЕуЮЊЯвЕФЯвШ§НЧЕФУцЛ§ШЁЕУзюДѓжЕЪБЃЌЯвзЖЕФКсзјБъгаКЮЙцТЩЃП
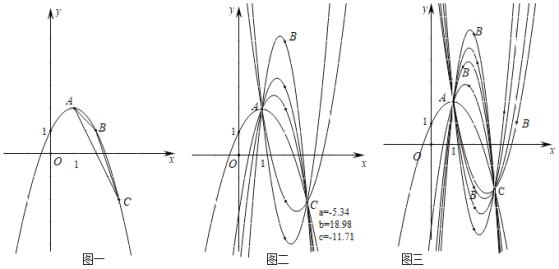
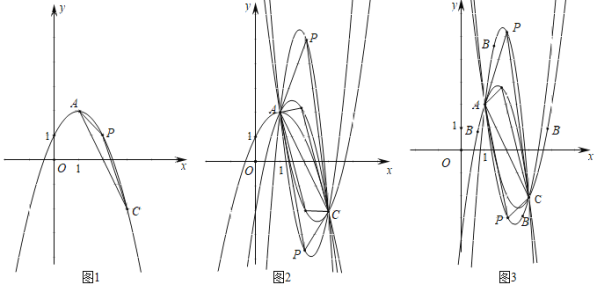
ЁОД№АИЁПЃЈ1ЃЉyЃНЉx2+2x+1ЃЌk1ЃН2ЃЛЃЈ2ЃЉyЃНЉnx2+ЃЈ4nЉ2ЃЉx+ЃЈ4Љ3nЃЉЃЌk2ЃН2ЃЌk1ЃНk2ЃЛЃЈ3ЃЉ![]() ЃЌk3ЃН2ЃЌЯвзЖЕФКсзјБъОљЯрЕШЃЎ
ЃЌk3ЃН2ЃЌЯвзЖЕФКсзјБъОљЯрЕШЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнД§ЖЈЯЕЪ§ЗЈЧѓНтМДПЩЃЛЙ§ЕуPзїPDЁЭxжсгкЕуDЃЌНЛжБЯпACгкЕуEЃЌШчЭМ4ЃЌвзЧѓГіжБЯпACЕФНтЮіЪНЃЌгЩгкЕуPЕФКсзјБъЮЊk1ЃЌдђЦфзнзјБъКЭЕуEЕФзнзјБъПЩЕУЃЌгкЪЧPEЕФГЄПЩгУk1ЕФДњЪ§ЪНБэЪОЃЌШЛКѓРћгУ![]() ПЩЕУЁїPACЕФУцЛ§Йигкk1ЕФКЏЪ§ЙиЯЕЪНЃЌдйРћгУЖўДЮКЏЪ§ЕФаджЪЧѓНтМДПЩЃЛ
ПЩЕУЁїPACЕФУцЛ§Йигкk1ЕФКЏЪ§ЙиЯЕЪНЃЌдйРћгУЖўДЮКЏЪ§ЕФаджЪЧѓНтМДПЩЃЛ
ЃЈ2ЃЉЯШИљОнД§ЖЈЯЕЪ§ЗЈЧѓГіХзЮяЯпЕФНтЮіЪНЃЌИљОнЕуBЕФЮЛжУашЗжЧщПіЬжТлЃКЂйШєn>0ЃЌШчЭМ4ЃЌЗТЃЈ1ЃЉЬтЕФЫМТЗгУk2ЕФДњЪ§ЪНБэЪОГіPEЕФГЄЃЌШЛКѓРћгУ![]() ПЩЕУЁїPACЕФУцЛ§Йигкk2ЕФКЏЪ§ЙиЯЕЪНЃЌдйРћгУЖўДЮКЏЪ§ЕФаджЪЧѓНтМДПЩЃЛЂкШєn<0ЃЌШчЭМ5ЃЌЗТЂйЕФЫМТЗПЩЕУ
ПЩЕУЁїPACЕФУцЛ§Йигкk2ЕФКЏЪ§ЙиЯЕЪНЃЌдйРћгУЖўДЮКЏЪ§ЕФаджЪЧѓНтМДПЩЃЛЂкШєn<0ЃЌШчЭМ5ЃЌЗТЂйЕФЫМТЗПЩЕУ![]() ЃЌНјЖјПЩгУk2ЕФДњЪ§ЪНБэЪОГіЁїPACЕФУцЛ§ЃЌдйРћгУЖўДЮКЏЪ§ЕФаджЪЧѓНтМДПЩЃЛНјвЛВНМДПЩБШНЯk1гыk2ЕФЪ§СПЙиЯЕЃЛ
ЃЌНјЖјПЩгУk2ЕФДњЪ§ЪНБэЪОГіЁїPACЕФУцЛ§ЃЌдйРћгУЖўДЮКЏЪ§ЕФаджЪЧѓНтМДПЩЃЛНјвЛВНМДПЩБШНЯk1гыk2ЕФЪ§СПЙиЯЕЃЛ
ЃЈ3ЃЉЯШИљОнД§ЖЈЯЕЪ§ЗЈЧѓГіХзЮяЯпЕФНтЮіЪНЃЌШЛКѓЗТЃЈ2ЃЉЬтЕФЫМТЗЗжСНжжЧщПіПЩЕУЁїPACЕФУцЛ§Йигкk3ЕФКЏЪ§ЙиЯЕЪНЃЌдйРћгУЖўДЮКЏЪ§ЕФаджЪЧѓНтМДПЩЃЌШЛКѓИљОнЧАУц3ИіаЁЬтЕФНсЙћМДПЩЕУГіЯвзЖЕФКсзјБъЕФЙцТЩЃЎ
НтЃКЩшХзЮяЯпЕФНтЮіЪНЮЊyЃНax2+bx+cЃЌ
ЃЈ1ЃЉЕБmЃН2ЃЌnЃН1ЪБЃЌАбAЃЈ1ЃЌ2ЃЉЁЂBЃЈ2ЃЌ1ЃЉЁЂCЃЈ3ЃЌЉ2ЃЉДњШыЃЌЕУ ЃЌНтЕУЃК
ЃЌНтЕУЃК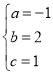 ЃЌ
ЃЌ
ЁрХзЮяЯпЕФНтЮіЪНЮЊЃКyЃНЉx2+2x+1ЃЌ
ЁпAЃЈ1ЃЌ2ЃЉЁЂCЃЈ3ЃЌЉ2ЃЉЃЌЁржБЯпACЕФНтЮіЪНЮЊyЃНЉ2x+4ЃЌ
ЁпPЃЈk1ЃЌЉk12+2k1+1ЃЉЃЌЙ§ЕуPзїPDЁЭxжсгкЕуDЃЌНЛжБЯпACгкЕуEЃЌШчЭМ4ЃЌдђЕуEЃЈk1ЃЌЉ2k1+4ЃЉЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁрЕБk1ЃН2ЪБЃЌЁїPACЕФУцЛ§зюДѓЃЛ

ЃЈ2ЃЉЕБmЃН2ЃЌnЁй1ЪБЃЌАбAЃЈ1ЃЌ2ЃЉЁЂBЃЈ2ЃЌnЃЉЁЂCЃЈ3ЃЌЉ2ЃЉДњШыЃЌЕУЃК
 ЃЌНтЕУЃК
ЃЌНтЕУЃК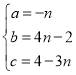 ЃЌ
ЃЌ
ЁрХзЮяЯпЕФНтЮіЪНЮЊЃКyЃНЉnx2+ЃЈ4nЉ2ЃЉx+ЃЈ4Љ3nЃЉЃЌ
ЂйШєn>0ЃЌЁпPЃЈk2ЃЌЉnk22+ЃЈ4nЉ2ЃЉk2+(4Љ3n)ЃЉЃЌЙ§ЕуPзїPDЁЭxжсгкЕуDЃЌНЛжБЯпACгкЕуEЃЌШчЭМ4ЃЌдђЕуEЃЈk2ЃЌЉ2k2+4ЃЉЃЌ
Ёр![]() =Љnk22+ЃЈ4nЉ2ЃЉk2+(4Љ3n)+2k2Ѓ4=Љnk22+4nk2Љ3nЃЌ
=Љnk22+ЃЈ4nЉ2ЃЉk2+(4Љ3n)+2k2Ѓ4=Љnk22+4nk2Љ3nЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁрЕБk2ЃН2ЪБЃЌЁїPACЕФУцЛ§зюДѓЃЛ
ЂкШєn<0ЃЌШчЭМ5ЃЌдђ![]() =Љ2k2+4+nk22ЃЃЈ4nЉ2ЃЉk2Ѓ(4Љ3n)=nk22Ѓ4nk2+3nЃЌ
=Љ2k2+4+nk22ЃЃЈ4nЉ2ЃЉk2Ѓ(4Љ3n)=nk22Ѓ4nk2+3nЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁрЕБk2ЃН2ЪБЃЌЁїPACЕФУцЛ§зюДѓЃЛ
злЩЯЃЌЕБk2ЃН2ЪБЃЌЁїPACЕФУцЛ§зюДѓЃЛ
Ёрk1ЃНk2ЃЛ

ЃЈ3ЃЉЕБmЁй2ЃЌnЁй1ЪБЃЌАбAЃЈ1ЃЌ2ЃЉЁЂBЃЈmЃЌnЃЉЁЂCЃЈ3ЃЌЉ2ЃЉДњШыЃЌЕУЃК
 ЃЌНтЕУЃК
ЃЌНтЕУЃК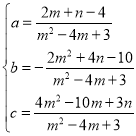 ЃЌ
ЃЌ
ЁрХзЮяЯпЕФНтЮіЪНЮЊЃК![]() ЃЌ
ЃЌ
дђPЃЈk3ЃЌ![]() ЃЉЃЌ
ЃЉЃЌ
ЂйШє![]() ЃЌЙ§ЕуPзїPDЁЭxжсгкЕуDЃЌНЛжБЯпACгкЕуEЃЌШчЭМ4ЃЌдђЕуEЃЈk3ЃЌЉ2k3+4ЃЉЃЌ
ЃЌЙ§ЕуPзїPDЁЭxжсгкЕуDЃЌНЛжБЯпACгкЕуEЃЌШчЭМ4ЃЌдђЕуEЃЈk3ЃЌЉ2k3+4ЃЉЃЌ
Ёр![]() =
=![]() =
=![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁрЕБk3ЃН2ЪБЃЌЁїPACЕФУцЛ§зюДѓЃЛ
ЂкШє![]() ЃЌШчЭМ5ЃЌдђ
ЃЌШчЭМ5ЃЌдђ![]() =
=![]()
![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁрЕБk3ЃН2ЪБЃЌЁїPACЕФУцЛ§зюДѓЃЛ
злЩЯЃЌЕБk3ЃН2ЪБЃЌЁїPACЕФУцЛ§зюДѓЃЛ
злЩЯЫљЪіЃЌЙ§ЖЈЕуAЁЂCЃЌИљОнBдкИїжжВЛЭЌЮЛжУЫљЕУМЦЫуНсЙћЃЌПЩвдЗЂЯжЭЈЙ§СНИіЖЈЕуЕФХзЮяЯпЯЕжаЃЌвдДЫСНЕуЮЊЯвЕФЯвШ§НЧЕФУцЛ§ШЁЕУзюДѓжЕЪБЃЌЯвзЖЕФКсзјБъОљЯрЕШЃЎ


 НзЬнМЦЫуЯЕСаД№АИ
НзЬнМЦЫуЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌPЪЧЕШбќжБНЧЁїABCЭтвЛЕуЃЌАбBPШЦЕуBЫГЪБеыа§зЊ90ЁуЕНBPЁфЃЌЪЙЕуPЁфдкЁїABCФкЃЌвбжЊЁЯAPЁфBЃН135ЁуЃЌШєСЌНгPЁфCЃЌPЁфAЃКPЁфCЃН1ЃК4ЃЌдђPЁфAЃКPЁфBЃНЃЈЁЁЁЁЃЉ

A.1ЃК4B.1ЃК5C.2ЃК![]() D.1ЃК
D.1ЃК![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊХзЮяЯпyЃНx2+bxЉ3ОЙ§ЕуAЃЈ1ЃЌ0ЃЉЃЌЖЅЕуЮЊЕуMЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФБэДяЪНМАЖЅЕуMЕФзјБъЃЛ
ЃЈ2ЃЉЧѓЁЯOAMЕФе§ЯвжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЈ1ЃЉЪЧФГЙЋдАРяЕФвЛжжНЁЩэЦїВФЃЌЦфВрУцЪОвтЭМШчЭМЃЈ2ЃЉЫљЪОЃЌЦфжаAB=AC=120cmЃЌBC=80cmЃЌAD=30cmЃЌЁЯDAC=90ЁуЃЎЧѓЕуDЕНЕиУцЕФИпЖШЪЧЖрЩйЃП

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
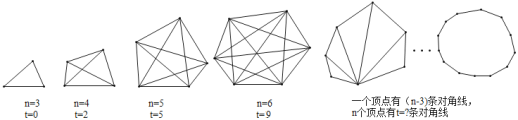
ЁОЬтФПЁПШчЭМЃЌЯШбаОПЯТУцШ§НЧаЮЁЂЫФБпаЮЁЂЮхБпаЮЁЂСљБпаЮЁЖрБпаЮЕФБпЪ§nМАЦфЖдНЧЯпЬѕЪ§tЕФЙиЯЕЃЌдйЭъГЩЯТУцЮЪЬтЃК
ЃЈ1ЃЉШєвЛИіЖрБпаЮЪЧЦпБпаЮЃЌЫќЕФЖдНЧЯпЬѕЪ§ЮЊЁЁ ЁЁЃЌnБпаЮЕФЖдНЧЯпЬѕЪ§ЮЊtЃНЁЁ ЁЁЃЈгУnБэЪОЃЉЃЎ
ЃЈ2ЃЉЧѓе§КУ65ЬѕЖдНЧЯпЕФЖрБпаЮЪЧМИБпаЮЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПаЁУїКЭаЁССЭцвЛИігЮЯЗЃКШ§еХДѓаЁЁЂжЪЕиЖМЯрЭЌЕФПЈЦЌЩЯЗжБ№БъгаЪ§зж2ЃЌ3ЃЌ4ЃЈБГУцЭъШЋЯрЭЌЃЉЃЌЯжНЋБъгаЪ§зжЕФвЛУцГЏЯТЃЎаЁУїДгжаШЮвтГщШЁвЛеХЃЌМЧЯТЪ§зжКѓЗХЛиЯДдШЃЌШЛКѓаЁССДгжаШЮвтГщШЁвЛеХЃЌМЦЫуаЁУїКЭаЁССГщЕУЕФСНИіЪ§зжжЎКЭЃЎШєКЭЮЊЦцЪ§ЃЌдђаЁУїЪЄЃЛШєКЭЮЊХМЪ§ЃЌдђаЁССЪЄЃЎ
ЃЈ1ЃЉЧыФугУЛЪїзДЭМЛђСаБэЕФЗНЗЈЃЌЧѓГіетСНЪ§КЭЮЊ6ЕФИХТЪЃЎ
ЃЈ2ЃЉФуШЯЮЊетИігЮЯЗЙцдђЖдЫЋЗНЙЋЦНТ№ЃПЫЕЫЕФуЕФРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
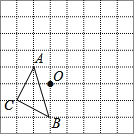
ЁОЬтФПЁПдкШчЭМЫљЪОЕФЗНИёжНжаЃЌУПИіаЁЗНИёЖМЪЧБпГЄЮЊ1ИіЕЅЮЛГЄЖШЕФе§ЗНаЮЃЌЁїABCЕФЖЅЕуМАЕуOЖМдкИёЕуЩЯЃЈУПИіаЁЗНИёЕФЖЅЕуНазіИёЕуЃЉЃЎ
ЃЈ1ЃЉвдЕуOЮЊЮЛЫЦжааФЃЌдкЭјИёЧјгђФкЛГіЁїAЁфBЁфCЁфЃЌЪЙЁїAЁфBЁфCЁфгыЁїABCЮЛЫЦЃЈAЁфЁЂBЁфЁЂCЁфЗжБ№ЮЊAЁЂBЁЂCЕФЖдгІЕуЃЉЃЌЧвЮЛЫЦБШЮЊ2ЃК1ЃЛ
ЃЈ2ЃЉЁїAЁфBЁфCЁфЕФУцЛ§ЮЊЁЁ ЁЁИіЦНЗНЕЅЮЛЃЛ
ЃЈ3ЃЉШєЭјИёжагавЛИёЕуDЁфЃЈвьгкЕуCЁфЃЉЃЌЧвЁїAЁфBЁфDЁфЕФУцЛ§ЕШгкЁїAЁфBЁфCЁфЕФУцЛ§ЃЌЧыдкЭМжаБъГіЫљгаЗћКЯЬѕМўЕФЕуDЁфЃЎЃЈШчЙћетбљЕФЕуDЁфВЛжЙвЛИіЃЌЧыгУD1ЁфЁЂD2ЁфЁЂЁЁЂDnЁфБъГіЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌABЪЧЁбOЕФжБОЖЃЌЯвCDЁЭABгкHЃЌЙ§CDбгГЄЯпЩЯвЛЕуEзїЁбOЕФЧаЯпНЛABЕФбгГЄЯпгкFЃЎЧаЕуЮЊGЃЌСЌНгAGНЛCDгкKЃЎ
ЃЈ1ЃЉШчЭМ1ЃЌЧѓжЄЃКKE=GEЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌШєACЁЮEFЃЌЪдХаЖЯЯпЖЮKGЁЂKDЁЂGEМфЕФЪ§СПЙиЯЕЃЌВЂЫЕУїРэгЩЃЛ
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТЃЌШєsinE=![]() ЃЌAK=2
ЃЌAK=2![]() ЃЌЧѓЁбOЕФАыОЖЃЎ
ЃЌЧѓЁбOЕФАыОЖЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃЌШчЭМЃЌгавЛПщКЌга30ЁуЕФжБНЧШ§НЧаЮ![]() ЕФжБНЧБп
ЕФжБНЧБп![]() ЕФГЄЧЁгыСэвЛПщЕШбќжБНЧШ§НЧаЮ
ЕФГЄЧЁгыСэвЛПщЕШбќжБНЧШ§НЧаЮ![]() ЕФаББп
ЕФаББп![]() ЕФГЄЯрЕШЃЎАбИУЬзШ§НЧАхЗХжУдкЦНУцжБНЧзјБъЯЕжаЃЌЧв
ЕФГЄЯрЕШЃЎАбИУЬзШ§НЧАхЗХжУдкЦНУцжБНЧзјБъЯЕжаЃЌЧв![]()
ЃЈ1ЃЉШєФГПЊПкЯђЯТЕФХзЮяЯпЕФЖЅЕуЧЁКУЮЊЕу![]() ЃЌЧыаДГівЛИіТњзуЬѕМўЕФХзЮяЯпЕФНтЮіЪНЃЎ
ЃЌЧыаДГівЛИіТњзуЬѕМўЕФХзЮяЯпЕФНтЮіЪНЃЎ
ЃЈ2ЃЉШєАбКЌ30ЁуЕФжБНЧШ§НЧаЮШЦЕу![]() АДЫГЪБеыЗНЯђа§зЊКѓЃЌаББп
АДЫГЪБеыЗНЯђа§зЊКѓЃЌаББп![]() ЧЁКУгыжсжиЕўЃЌЕу
ЧЁКУгыжсжиЕўЃЌЕу![]() ТфдкЕу
ТфдкЕу![]() ЃЌЪдЧѓЭМжавѕгАВПЗжЕФУцЛ§ЃЈНсЙћБЃСє
ЃЌЪдЧѓЭМжавѕгАВПЗжЕФУцЛ§ЃЈНсЙћБЃСє![]() ЃЉ
ЃЉ

ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com