
 如图,将矩形纸片ABCD沿直线AE折叠,点B恰好落在线段CD的中点F上,点G是线段AF上一动点(不与A,F重合),点G过GH⊥AB,垂足为H,将矩形沿直线GH翻折,点A恰好落在线段BH上点A′处.若AB长为8,则当△A′GE为直角三角形时,AH的长为$\frac{24-8\sqrt{3}}{3}$.
如图,将矩形纸片ABCD沿直线AE折叠,点B恰好落在线段CD的中点F上,点G是线段AF上一动点(不与A,F重合),点G过GH⊥AB,垂足为H,将矩形沿直线GH翻折,点A恰好落在线段BH上点A′处.若AB长为8,则当△A′GE为直角三角形时,AH的长为$\frac{24-8\sqrt{3}}{3}$. 分析 根据翻转的性质可知△ABE≌△AFE,由于AF=AB=8,EF=BE,∠2=∠3,于是得到DC=AB=8,BC=AD,根据勾股定理得到BC=AD=$\sqrt{A{F}^{2}{-DF}^{2}}$=$\sqrt{{8}^{2}-{4}^{2}}$=4$\sqrt{3}$,根据已知求得∠1=∠2=30°,设BE=x,则EF=x,CE=4$\sqrt{3}$-x,由勾股定理列方程解得BE=x=$\frac{8\sqrt{3}}{3}$,根据折叠的性质得到AG=A′G,AH=A′H,证出△AGA′是等边三角形,推出△AGE≌△AA′E,得到GE=A′E,当△A′GE是直角三角形时,只能∠A′EG=90°,于是得到△A′EG是等腰直角三角形,设AH=y,则AA′=A′G=2y,A′B=AB=AB-AA′=8-2y,再根据勾股定理列方程即可得到结果.
解答 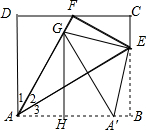 解:如图所示,根据翻转的性质可知:△ABE≌△AFE,
解:如图所示,根据翻转的性质可知:△ABE≌△AFE,
∵AF=AB=8,EF=BE,∠2=∠3,
有已知得:DC=AB=8,BC=AD,
∵F是DC的中点,DF=CF=$\frac{1}{2}$DC=4,
∴BC=AD=$\sqrt{A{F}^{2}{-DF}^{2}}$=$\sqrt{{8}^{2}-{4}^{2}}$=4$\sqrt{3}$,
∵∠D=90°,AF=2DF,
∴∠1=30°,
∴∠BAF=60°,
∴∠1=∠2=30°,
设BE=x,则EF=x,CE=4$\sqrt{3}$-x,
在Rt△CEF中,EF2=CE2+CF2,
即${x}^{2}=(4\sqrt{3}-x)^{2}+16$,
解得:BE=x=$\frac{8\sqrt{3}}{3}$,
∵矩形沿GH翻折,点A落在线段BH上点A′处,
∴AG=A′G,AH=A′H,
∵∠BAF=60°,
∴△AGA′是等边三角形,
∴AG=AA′,
在△AGE与△AA′E中,$\left\{\begin{array}{l}{AG=AA′}\\{∠2=∠3}\\{AE=AE}\end{array}\right.$,
∴△AGE≌△AA′E,
∴GE=A′E,
∴当△A′GE是直角三角形时,只能∠A′EG=90°,
∴△A′EG是等腰直角三角形,设AH=y,则AA′=A′G=2y,A′B=AB=AB-AA′=8-2y,
在等腰直角三角形A′GE中,A′E=$\frac{\sqrt{2}}{2}$A′G=$\sqrt{2}$y,
在直角三角形A′BE中,A′E=$\sqrt{A′{B}^{2}+B{E}^{2}}$=$\sqrt{(8-2y)^{2}+(\frac{8\sqrt{3}}{3})^{2}}$,
2y2=(8-2y)2+($\frac{8\sqrt{3}}{3}$)2
解得:y1=$\frac{24-8\sqrt{3}}{3}$,y2=8$+\frac{8\sqrt{3}}{3}$(不合题意舍去),
∴AH=$\frac{24-8\sqrt{3}}{3}$,
故答案为:$\frac{24-8\sqrt{3}}{3}$.
点评 本题考查了翻折变换-折叠问题,全等三角形的判定和性质,勾股定理,等腰三角形的性质,等腰直角三角形的性质,熟练掌握折叠的性质是解题的关键.


科目:初中数学 来源: 题型:填空题
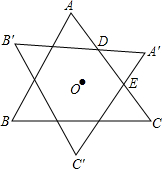 如图,将等边三角形ABC绕其外心O顺时针旋转α(0°<α<120°)至△A′B′C′,交AC于点D,E,若以AD,DE,EC为三边所围成的三角形为直角三角形,则旋转角α=30°或90°.
如图,将等边三角形ABC绕其外心O顺时针旋转α(0°<α<120°)至△A′B′C′,交AC于点D,E,若以AD,DE,EC为三边所围成的三角形为直角三角形,则旋转角α=30°或90°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,某农场有一块四边形ABCD的空地,其各边中点分别是E、F、G、H,测得对角线AC=BD=12米,现想用篱笆围成四边形EFGH的场地,则需用的篱笆总长度是( )
如图,某农场有一块四边形ABCD的空地,其各边中点分别是E、F、G、H,测得对角线AC=BD=12米,现想用篱笆围成四边形EFGH的场地,则需用的篱笆总长度是( )| A. | 12米 | B. | 24米 | C. | 36米 | D. | 48米 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图所示,在?ABCD中,E是BC边上的三分之一点,则S△ABC:S?ABCD的值为( )
如图所示,在?ABCD中,E是BC边上的三分之一点,则S△ABC:S?ABCD的值为( )| A. | ${\;}_{\frac{1}{2}}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{8}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com