
【题目】如图,△ABC和△DEF均是边长为4的等边三角形,△DEF的顶点D为△ABC的一边BC的中点,△DEF绕点D旋转,且边DF,DE始终分别交△ABC的边AB,AC于点H,G,图中直线BC两侧的图形关于直线BC成轴对称.连结HH′,HG,GG′,H′G′,其中HH′、GG′分别交BC于点I,J.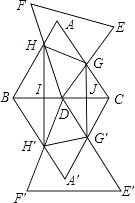
(1)求证:△DHB∽△GDC;
(2)设CG=x,四边形HH′G′G的面积为y,
①求y关于x的函数解析式和自变量x的取值范围.
②求当x为何值时,y的值最大,最大值为多少?
【答案】
(1)
证明:在正△ABC中,∠ABC=∠ACB=60°,
∴∠BHD+∠BDH=120°,
在正△DEF中,∠EDF=60°,
∴∠GDC+∠BDH=120°,
∴∠BHD=∠GDC,
∴△DHB∽△GDC
(2)
证明:①∵D为BC的中点,
∴BD=CD=2,
由△DHB∽△GDC,
∴ ![]() ,
,
即: ![]() ,
,
∴BH= ![]() ,
,
∵H,H′和G,G′关于BC对称,
∴HH′⊥BC,GG′⊥BC,
∴在Rt△BHI中,BI= ![]() BH=
BH= ![]() ,HI=
,HI= ![]() BH=
BH= ![]()
![]() ,
,
在Rt△CGJ中,CJ= ![]() CG=
CG= ![]() ,GJ=
,GJ= ![]() CG=
CG= ![]()
![]() ,
,
∴HH′=2HI= ![]() ,GG’=2GJ=
,GG’=2GJ= ![]() x,IJ=4﹣
x,IJ=4﹣ ![]() ﹣
﹣ ![]() ,
,
∴y= ![]() (
( ![]() +
+ ![]() x)(4﹣
x)(4﹣ ![]() ﹣
﹣ ![]() )
)
∵边DF、DE始终分别交△ABC的边AB、AC于点H、G,
∴当△DEF绕点D旋转时,点H和A重合时,AG=3,
∴x=CG=1,
当点G和A重合时,CG=4,
∴x=4,
∴1≤x≤4
②由①得,y=﹣ ![]() (
( ![]() +x)2+2
+x)2+2 ![]() (
( ![]() +x),
+x),
设 ![]() =a,得y=﹣
=a,得y=﹣ ![]() a2+2
a2+2 ![]() a,
a,
当a=4时,y最大=4 ![]() ,
,
此时 ![]() =4,解得x=2.
=4,解得x=2.
【解析】(1)由等边三角形的特点得到相等关系,即可;(2)由相似三角形得到 ![]() ,再结合对称,表示出相关的线段,四边形HH′G′G的面积为y求出即可.
,再结合对称,表示出相关的线段,四边形HH′G′G的面积为y求出即可.


 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案科目:初中数学 来源: 题型:
【题目】小明到服装店进行社会实践活动,服装店经理让小明帮助解决以下问题:服装店准备购进甲乙两种服装,甲种每件进价80元,售价120元,乙种每件进价60元,售价90元.计划购进两种服装共100件,其中甲种服装不少于65件.
(1)若购进这100件服装的费用不得超过7500元,则甲种服装最多购进多少件??
(2)在(1)的条件下,该服装店对甲种服装以每件优惠a(0<a<20)元的价格进行促销活动,乙种服装价格不变,那么该服装店应如何调整进货方案才能获得最大利润?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连接BD、DP,BD与CF相交于点H.给出下列结论:
①△ABE≌△DCF;② ![]() ;③DP2=PHPB;④
;③DP2=PHPB;④ ![]() .
.
其中正确的是 . (写出所有正确结论的序号)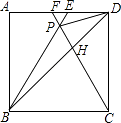
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明有一个呈等腰直角三角形的积木盒,现在积木盒中只剩下如图1所示的九个空格,图2是可供选择的A,B,C,D四块积木. 
(1)小明选择把积木A和B放入图3,要求积木A和B的九个小圆恰好能分别与图3中的九个小圆重合,请在图3中画出他放入方式的示意图(温馨提醒:积木A和B的连接小圆的小线段还是要画上哦!);
(2)现从A、B、C、D四块积木中任选两块,请用列表法或画树状图法求恰好能全部不重叠放入的概率
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】写出下列命题的已知、求证,并完成证明过程.
命题:如果一个三角形的两条边相等,那么两条边所对的角也相等(简称:“等边对等角”.)
(1)已知: .
求证: .
(2)证明:“等边对等角”
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+bx+c与x轴相交于A、B两点,与y轴相交于点C,且点B与点C的坐标分别为B(3,0).C(0,3),点M是抛物线的顶点.
(1)求二次函数的关系式;
(2)点P为线段MB上一个动点,过点P作PD⊥x轴于点D.若OD=m,△PCD的面积为S,试判断S有最大值或最小值?并说明理由;
(3)在MB上是否存在点P,使△PCD为直角三角形?如果存在,请直接写出点P的坐标;如果不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com