
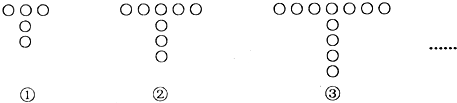
分析 (1)通过观察已知图形可得:每个图形都比其前一个图形多3枚棋子,得出摆成第十个图案需要的棋子数;
(2)由(1)得出规律为摆成第n个图案需要3n+2枚棋子;
(3)由(2)中规律求出即可.
解答 解:(1)∵第一个“T”字图案需要3+2=5枚棋子,第二个“T”字图案需要3×2+2=8枚棋子,第三个“T”字图案需要3×3+2=11枚棋子,…
∴第n个图案需要5+3(n-1)=3n+2.
那么当n=10时,则有32枚;
故摆成第十个图案需要32枚棋子.
(2)第n个图案需5+3×(n-1)=5+3n-3=(3n+2)枚棋子.
(3)3×2013+2=6041(枚),
即第2013个图案需6041枚棋子.
故答案为:(1)32枚;(2)(3n+2)枚;(3)6041枚.
点评 此题考查图形的变化规律,注意由特殊到一般的分析方法,得出数字变化规律是解题关键.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
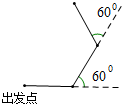 如图,小华在空旷的操场上向右行走20米后,接着向左转60°,再向前行走20米,再接着向左转,再向前行走20米,…这样一直走下去.
如图,小华在空旷的操场上向右行走20米后,接着向左转60°,再向前行走20米,再接着向左转,再向前行走20米,…这样一直走下去.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 请你在方格纸上按照如下要求设计直角三角形,所作三角形的各个顶点均在格点上:
请你在方格纸上按照如下要求设计直角三角形,所作三角形的各个顶点均在格点上:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -22=4 | B. | $\frac{2^2}{3}=\frac{4}{9}$ | C. | $({-3.5})-({-5\frac{1}{2}})=2$ | D. | $({-\frac{1}{2}})-|{-\frac{1}{2}}|=0$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com