
【题目】如图,![]() 中,
中,![]() 边上的高
边上的高![]() ,点
,点![]() 在
在![]() 上,且
上,且![]() ,点
,点![]() 在
在![]() 上,过点
上,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,当点
,当点![]() 在高
在高![]() 上移动时,点
上移动时,点![]() 可左右移动的最大距离是__________.
可左右移动的最大距离是__________.

【答案】4
【解析】
先求出AB及∠BAD=∠ABC=45°,当点F与点A重合时,DG=AD=3,即点G在点D右侧时最大值为3,过点E作EH⊥AD于H,设DG=y,DF=x,则FH=2-x,证明△EFH∽△FGD,得到![]() ,求出
,求出![]() ,当x=1时,y有最大值1,即点G在点D左侧时最大值为1,由此得到点G左右移动的距离.
,当x=1时,y有最大值1,即点G在点D左侧时最大值为1,由此得到点G左右移动的距离.
∵![]() ,
,
∴∠ADC=∠ADB=90°,
∵∠ABC=45°,
∴∠BAD=∠ABC=45°,
∴BD=AD=3,
∴CD=AB-BD=7-3=4,![]() ,
,
∵![]() ,
,
∴AE=![]() ,
,
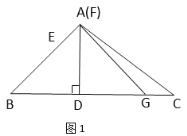
当点F与点A重合时,如图1,
∵∠EFG=90°,
∴∠DAG=∠AGD=45°,
∴DG=AD=3,即点G在点D右侧时最大值为3,
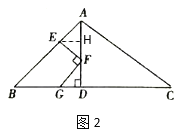
当点F向下移动到最低位置时,如图2,过点E作EH⊥AD于H,
∴AH=EH=1,∠EHF=90°,
∴DH=AD-AH=2,
设DG=y,DF=x,则FH=2-x,
∵∠EFG=90°,
∴∠EFH+∠GFD=90°,
∵∠HEF+∠EFH=90°,
∴∠HEF=∠GFD,
∵∠EHF=∠GDF=90°,
∴△EFH∽△FGD,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵-1<0,
∴当x=1时,y有最大值1,即点G在点D左侧时最大值为1,
∴点![]() 可左右移动的最大距离是3+1=4,
可左右移动的最大距离是3+1=4,
故答案为:4.


 全能测控一本好卷系列答案
全能测控一本好卷系列答案科目:初中数学 来源: 题型:
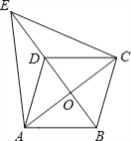
【题目】如图,在□ABCD中,对角线AC、BD相交于点O,点E在BD的延长线上,且△EAC是等边三角形.
(1)求证:四边形ABCD是菱形.
(2)若AC=8,AB=5,求ED的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与x轴交于点
与x轴交于点![]() ,点
,点![]() ,与y轴交于点C,且过点
,与y轴交于点C,且过点![]() .点P、Q是抛物线
.点P、Q是抛物线![]() 上的动点.
上的动点.
(1)求抛物线的解析式;
(2)当点P在直线OD下方时,求![]() 面积的最大值.
面积的最大值.
(3)直线OQ与线段BC相交于点E,当![]() 与
与![]() 相似时,求点Q的坐标.
相似时,求点Q的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=5,BC=4![]() ,D为边AB上一动点(B点除外),以CD为一边作正方形CDEF,连接BE,则△BDE面积的最大值为______.
,D为边AB上一动点(B点除外),以CD为一边作正方形CDEF,连接BE,则△BDE面积的最大值为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AB是半径为1的圆O直径,C是圆上一点,D是BC延长线上一点,过点D的直线交AC于E点,交AB于点F,DF=BF,EA=EF.

(1)求证:△AEF为等边三角形;
(2)若CF⊥AB,①试说明DC = CF;②求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)问题发现
如图①,![]() 是等腰直角三角形,四边形
是等腰直角三角形,四边形![]() 是正方形,点
是正方形,点![]() 与点
与点![]() 重合,则线段
重合,则线段![]() 与
与![]() 之间的数量关系和位置关系分别是 .
之间的数量关系和位置关系分别是 .
(2)深入探究
如图②,![]() 是等腰直角三角形,四边形
是等腰直角三角形,四边形![]() 是正方形,点
是正方形,点![]() 在直线
在直线![]() 上,对角线
上,对角线![]() 所在的直线交直线
所在的直线交直线![]() 于点
于点![]() ,则线段
,则线段![]() 之间有什么数量关系?请仅就图②给出证明.
之间有什么数量关系?请仅就图②给出证明.
(3)拓展思维
如图②,若点![]() 在直线
在直线![]() 上,且线段
上,且线段![]() ,当
,当![]() 时,直接写出此时正方形
时,直接写出此时正方形![]() 的面积.
的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在直角坐标系中,直线l与x、y轴分别交于点A(4,0)、B(0,![]() )两点,∠BAO的角平分线交y轴于点D. 点C为直线l上一点,以AC为直径的⊙G经过点D,且与x轴交于另一点E.
)两点,∠BAO的角平分线交y轴于点D. 点C为直线l上一点,以AC为直径的⊙G经过点D,且与x轴交于另一点E.
(1)求证:y轴是⊙G的切线;
(2)求出⊙G的半径r,并直接写出点C的坐标;
(3)如图2,若点F为⊙G上的一点,连接AF,且满足∠FEA=45°,请求出EF的长?
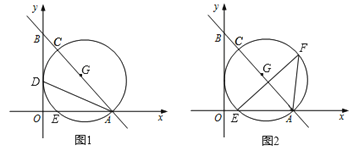
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种植户计划将一片荒山改良后种植沃柑,经市场调查得知,当种植沃柑的面积x不超过15亩时,每亩可获得利润y=1900元;超过15亩时,每亩获得利润y(元)与种植面积x(亩)之间的函数关系:y=kx+b,并且当x=20时,y=1800;当x=25时,y=1700.
(1)请求出y与x的函数关系式,并写出自变量的取值范围;
(2)设种植户种植x亩沃柑所获得的总利润为w元,由于受条件限制,种植沃柑面积x不超过50亩,求该种植户种植多少亩获得的总利润最大,并求总利润w(元)的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
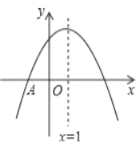
【题目】如图,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() ,顶点坐标
,顶点坐标![]() ,则下列结论:
,则下列结论:
①![]() ,
,![]() ,
,![]() ;②
;②![]() ;③关于
;③关于![]() 的方程
的方程![]() 有两个不相等的实数根;④
有两个不相等的实数根;④![]() .其中结论正确的是( )
.其中结论正确的是( )
A.①B.②③C.②④D.②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com