
【题目】如图,在四边形ABCD中,∠ABC=90°,AB=3,BC=4,DC=12,AD=13,求四边形ABCD的面积.

科目:初中数学 来源: 题型:
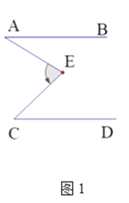
【题目】如图,AB∥CD.
(1)如图1,若∠A=35°,∠C=48°则∠E= °.
(2)如图2,若∠E=120°,∠C=110°,求∠A+∠F的度数;
(3)如图3,若∠E=110°,![]()
![]() ,若GD∥FC,请直接写出∠AGF与∠GDC的数量关系: .
,若GD∥FC,请直接写出∠AGF与∠GDC的数量关系: .


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是边长为6的等边三角形,P是AC边上一动点,由A向C运动(与A、C不重合),Q是CB延长线上一点,与点P同时以相同的速度由B向CB延长线方向运动(Q不与B重合),过P作PE⊥AB于E,连接PQ交AB于D.
(1)当∠BQD=30°时,求AP的长;
(2)当运动过程中线段ED的长是否发生变化?如果不变,求出线段ED的长;如果变化请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,AB⊥AC,AB=2,AC=4.对角线AC,BD相交于点O,将直线AC绕点O顺时针旋转α°,分别交直线BC、AD于点E、F.

(1)当α= °,四边形ABEF是平行四边形;
(2)在旋转的过程中,从A、B、C、D、E、F中任意4个点为顶点构造四边形.
①α= °,构造的四边形是菱形;
②若构造的四边形是矩形,求出该矩形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】码头工人每天往一艘轮船50吨货物,装载完毕恰好用了8天时间.
(1)轮船到达目的地后开始卸货,平均卸货速度v(单位:吨/天)与卸货时间t(单位:天)之间有怎样的函数关系?
(2)由于遇到紧急情况,要求船上的货物不超过5天卸货完毕,那么平均每天至少要卸多少吨货物?
(3)若原有码头工人10名,在(2)的条件下,至少需要增加多少名工人才能完成任务?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的袋子中装有若干个除颜色外均相同的小球,小明每次从袋子中摸出一个球,记录下颜色,然后放回,重复这样的试验1000次,记录结果如下:
实验次数n | 200 | 300 | 400 | 500 | 600 | 700 | 800 | 1000 |
摸到红球次数m | 151 | 221 | 289 | 358 | 429 | 497 | 568 | 701 |
摸到红球频率 | 0.75 | 0.74 | 0.72 | 0.72 | 0.72 | 0.71 | a | b |
(1)表格中a=________,b=_________;
(2)估计从袋子中摸出一个球恰好是红球的概率约为________;(精确到0.1)
(3)如果袋子中有14个红球,那么袋子中除了红球,还有多少个其他颜色的球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A1(1,0),A2(1,1),A3(-1,1),A4(-1,-1),A5(2,-1),…,则点A2 019的坐标为____________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,已知矩形纸片ABCD,AD=2,AB=4,将纸片折叠,使顶点A与边CD上的点E重合,折痕FG分别与AB、CD交于点G、F,AE与FG交于点O.
(1)如图1,求证:A、G、E、F四点围成的四边形是菱形;
(2)如图2,点N是线段BC的中点,且ON=OD,求折痕FG的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】说理填空:如图,点E是DC的中点,EC=EB,∠CDA=120°,DF//BE,且DF平分∠CDA,求证:△BEC为等边三角形.

解: 因为DF平分∠CDA(已知)
所以∠FDC=![]() ∠________. ( )
∠________. ( )
因为∠CDA=120°(已知)
所以∠FDC=______°.
因为DF//BE(已知)
所以∠FDC=∠_________.(____________________________________)
所以∠BEC = 60°,又因为EC=EB,(已知)
所以△BCE为等边三角形.(_____________________________)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com