
| A. | 2 | B. | 1 | C. | $\sqrt{2}$ | D. | $\frac{\sqrt{2}}{2}$ |
分析 根据抛物线解析式得到点A、B、C的坐标,然后利用勾股定理和三角形的面积公式进行解答.
解答 解:∵y=x2-bx(b≠0)的顶点为C,与x轴交于A、B两点,
∴A(0,0),B(b,0),C($\frac{b}{2}$,$\frac{{b}^{2}}{4}$).
∴AB=|b|,AC=$\sqrt{\frac{{b}^{2}}{4}+\frac{{b}^{4}}{16}}$,
又∵△ABC是等腰直角三角形,
∴AB2=2AC2,即b2=$\frac{{b}^{2}}{2}$+$\frac{{b}^{4}}{8}$.
解得b2=4,
则S△ABC=$\frac{1}{2}$AC2=$\frac{1}{4}$b2=1.
故选:B.
点评 本题考查了抛物线与x轴的交点坐标.解题的关键是熟悉等腰直角三角形的性质、勾股定理和三角形的面积公式.


 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案科目:初中数学 来源: 题型:解答题
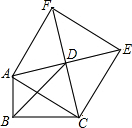 如图,在△ABC中,∠ABC=90°,以AC为一边向三角形外作菱形ACEF,D为菱形ACEF对角线的交点,连接BD,BD平分∠ABC.
如图,在△ABC中,∠ABC=90°,以AC为一边向三角形外作菱形ACEF,D为菱形ACEF对角线的交点,连接BD,BD平分∠ABC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 30 | B. | 40 | C. | 10$\sqrt{5}$ | D. | 20 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
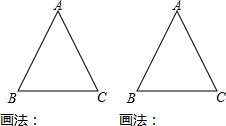 晓明有一把没有刻度的直角三角板,他要用这块三角板找出一个等腰三角形的对称轴,你能帮他完成吗?请用两种方法在图中画出等腰三角形的对称轴并注明方法.
晓明有一把没有刻度的直角三角板,他要用这块三角板找出一个等腰三角形的对称轴,你能帮他完成吗?请用两种方法在图中画出等腰三角形的对称轴并注明方法.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
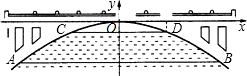 有一座抛物线形拱桥,如图所示,桥下面在正常水位时AB宽为20m,此时拱顶到水面的距离为4m,水位警戒线CD宽为10m.
有一座抛物线形拱桥,如图所示,桥下面在正常水位时AB宽为20m,此时拱顶到水面的距离为4m,水位警戒线CD宽为10m.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com