
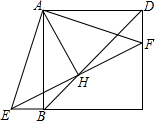
 已知四边形ABCD是正方形,F、E分别是DC和CB延长线上的点,且DF=BE,连接AE、AF、EF
已知四边形ABCD是正方形,F、E分别是DC和CB延长线上的点,且DF=BE,连接AE、AF、EF分析 (1)由正方形的性质得出∠ABC=∠ADF=∠BAD=90°,AB=AD,由SAS证明△ADF≌△ABE即可;
(2)由全等三角形的性质得出∠DAF=∠BAE,证出∠EAF=90°,即可得出答案;
(3)由全等三角形的性质得出∠EAF=90°,AE=AF,证出△AEF是等腰直角三角形,作FG⊥CD交BD于G,证出△DFG是等腰直角三角形,得出GF=DF=BE,由平行线得出△FGH∽△EBH,得出对应边成比例证出FH=EH,再由等腰直角三角形的性质即可得出结论.
解答 (1)证明:∵四边形ABCD是正方形,
∴∠ABC=∠ADF=∠BAD=90°,AB=AD,
∴∠ABE=90°,
在△ADF和△ABE中,$\left\{\begin{array}{l}{AD=AB}&{\;}\\{∠ADF=∠ABE}&{\;}\\{DF=BE}&{\;}\end{array}\right.$,
∴△ADF≌△ABE(SAS).
(2)解:由(1)得△ADF≌△ABE,
∴∠DAF=∠BAE,
∵∠DAF+∠BAF=90°,
∴∠BAE+∠BAF=90°,即∠EAF=90°,
∴△ABE可以看成是△ADF以点A为旋转中心,按顺时针方向旋转90度得到的;
故答案为:A,90;
(3)解:AH=$\frac{1}{2}$EF,AH⊥EF;理由如下:
由(1)得:∠EAF=90°,AE=AF,
∴△AEF是等腰直角三角形,
作FG⊥CD交BD于G,如图所示:
则FG∥BC,
∵四边形ABCD是平行四边形,
∴∠FDG=45°,
∴△DFG是等腰直角三角形,
∴GF=DF=BE,
∵FG∥BC,
∴△FGH∽△EBH,
∴FH:EH=GF:BE=1:1,
∴FH=EH,
∴AH=$\frac{1}{2}$EF,AH⊥EF.
点评 此题是四边形综合题目,考查了正方形的性质、全等三角形的判定与性质、等腰直角三角形的判定与性质、旋转的性质等知识;熟练掌握正方形的性质,证明三角形全等是解决问题的关键.


 学业测评一课一测系列答案
学业测评一课一测系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 投出的篮球会下落 | B. | 从装有黑球、白球的袋里摸出红球 | ||
| C. | 367人中至少有2人是同月同日出生 | D. | 买1张彩票,中500万大奖 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
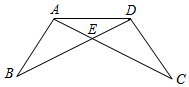 在一次数学课上,王老师在黑板上画出图,并写下了四个等式:①AB=DC,②BE=CE,③∠B=∠C,④∠BAE=∠CDE.要求同学从这四个等式中选出两个作为条件,推出∠CAD=∠BDA.请你试着完成王老师提出的要求,并说明理由.(写出一种即可)
在一次数学课上,王老师在黑板上画出图,并写下了四个等式:①AB=DC,②BE=CE,③∠B=∠C,④∠BAE=∠CDE.要求同学从这四个等式中选出两个作为条件,推出∠CAD=∠BDA.请你试着完成王老师提出的要求,并说明理由.(写出一种即可)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com