
【题目】在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F.

(1)求证:△AEF≌△DEB;
(2)证明四边形ADCF是菱形;
(3)若AC=4,AB=5,求菱形ADCF的面积.
【答案】(1)见解析;(2)见解析;(3)10.
【解析】
试题分析:(1)根据AAS证△AFE≌△DBE;
(2)利用①中全等三角形的对应边相等得到AF=BD.结合已知条件,利用“有一组对边平行且相等的四边形是平行四边形”得到ADCF是菱形,由“直角三角形斜边的中线等于斜边的一半”得到AD=DC,从而得出结论;
(3)由直角三角形ABC与菱形有相同的高,根据等积变形求出这个高,代入菱形面积公式可求出结论.
(1)证明:①∵AF∥BC,
∴∠AFE=∠DBE,
∵E是AD的中点,AD是BC边上的中线,
∴AE=DE,BD=CD,
在△AFE和△DBE中,
 ,
,
∴△AFE≌△DBE(AAS);
(2)证明:由(1)知,△AFE≌△DBE,则AF=DB.
∵DB=DC,
∴AF=CD.
∵AF∥BC,
∴四边形ADCF是平行四边形,
∵∠BAC=90°,D是BC的中点,E是AD的中点,
∴AD=DC=![]() BC,
BC,
∴四边形ADCF是菱形;
(3)解:设菱形DC边上的高为h,
∴RT△ABC斜边BC边上的高也为h,
∵BC=![]() =
=![]() ,
,
∴DC=![]() BC=
BC=![]() ,
,
∴h=![]() =
=![]() ,
,
菱形ADCF的面积为:DCh=![]() ×
×![]() =10.
=10.


科目:初中数学 来源: 题型:
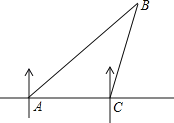
【题目】一船在A处测得北偏东45°方向有一灯塔B,船向正东方向以每小时20海里的速度航行1.5小时到达C处时,又观测到灯塔B在北偏东15°方向上,求此时航船与灯塔相距多少海里?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列调查中,最适合采用全面调查(普查)的是
A. 了解一批IPAD的使用寿命
B. 了解某鱼塘中鱼的数量
C. 了解某班学生对国家“一带一路”战略的知晓率
D. 了解电视栏目《朗读者》的收视率
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列计算正确的是( )
A. 2x2+3x2=5x4 B. ﹣5x2+(3x)2=4x2 C. 2x23x3=6x6 D. 2x2x3=4x5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两名学生10次立定跳远成绩的平均数相同,若甲10次立定跳远成绩的方差S甲2=0.006,乙10次立定跳远成绩的方差S乙2=0.035,则( )
A. 甲的成绩比乙的成绩稳定
B. 乙的成绩比甲的成绩稳定
C. 甲、乙两人的成绩一样稳定
D. 甲、乙两人成绩的稳定性不能比较
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为判断某运动员的成绩是否稳定,教练要对他10 次训练的成绩进行统计分析,则教练需了10 次成绩的
A. 众数 B. 方差 C. 平均数 D. 频数
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com