
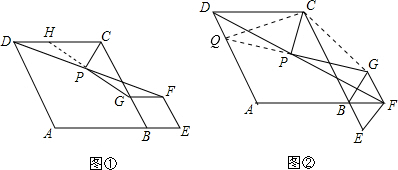
分析 (1)延长GP交DC于H,先证明△DHP≌△FGP,得出HP=GP,DH=FG=BG,证出CH=CG,PG⊥PC,再求出∠CGP=30°,即可得出结论;
(2)延长GP交AD于Q,连结CQ、CG,先证明△DQP≌△FGP,得出DQ=FG=BG,QP=GP,再证明△CDQ≌△CBG,得出∠DCQ=∠BCG,CQ=CG,证出PG⊥PC,求出∠CGP=30°,即可得出结论.
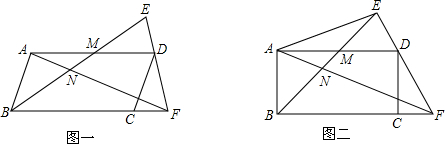
解答 (1)证明:延长GP交DC于H,如图①所示: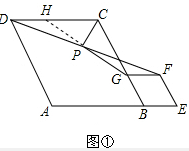
∵四边形ABCD和BEFG均为菱形,
∴DC=BC,GF=BG,DC∥AE∥GF,
∴∠HDP=∠GFP,∠DHP=∠FGP,
∵P是线段DF的中点,
∴DP=FP,
在△DHP和△FGP中,$\left\{\begin{array}{l}{∠HDP=∠GFP}&{\;}\\{∠DHP=∠FGP}&{\;}\\{DP=FP}&{\;}\end{array}\right.$,
∴△DHP≌△FGP(AAS),
∴HP=GP,DH=FG=BG,
∴CH=CG,
∴CP⊥HG,即PG⊥PC,
∵∠ABC═60°,
∴∠HCG=180°-60°=120°,
∴∠CGP=$\frac{1}{2}$(180°-120°)=30°,
∴PG=$\sqrt{3}$PC;
(2)成立;理由如下:延长GP交AD于Q,连结CQ、CG,如图②所示: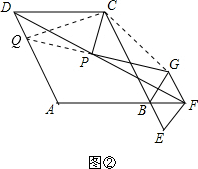
∵四边形ABCD和BEFG均为菱形,
∴DC=BC,GF=BG,DA∥CE∥GF,
∴∠DQP=∠FGP,∠QDP=∠GFP,
∵P是线段DF的中点,
∴DP=FP,
在△DQP和△FGP中,$\left\{\begin{array}{l}{∠DQP=∠FGP}&{\;}\\{∠QDP=∠GFP}&{\;}\\{DP=FP}&{\;}\end{array}\right.$,
∴△DQP≌△FGP(AAS),
∴DQ=FG=BG,QP=GP,
∵EF∥BG,
∴∠CBG=∠BEF=60°,
∵∠CDQ=∠ABC=60°,
∴∠CBG=∠CDQ,
在△CDQ和△CBG中,$\left\{\begin{array}{l}{CD=BC}&{\;}\\{∠CDQ=∠CBG}&{\;}\\{DQ=BG}&{\;}\end{array}\right.$,
∴△CDQ≌△CBG(SAS),
∴∠DCQ=∠BCG,CQ=CG,
∴CP⊥QG,即PG⊥PC,
∵∠DCB=180°-60°=120°,即∠DCQ+∠BCQ=120°,
∴∠BCG+∠BCQ=120°,即∠QCG=120°,
∴∠CGP=$\frac{1}{2}$(180°-120°)=30°,
∴PG=$\sqrt{3}$PC.
点评 本题考查了菱形的性质、全等三角形的判定与性质、含30°的直角三角形的性质以及旋转的性质;熟练掌握菱形的性质,证明三角形全等是解决问题的关键.


 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:初中数学 来源: 题型:解答题
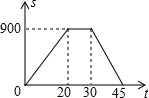 乐平街上新开张了一家“好又多”超市,这个星期天,张明和妈妈去这家新开张的超市买东西,如图反映了张明从家到超市的时间t(分钟)与距离s(米)之间关系的一幅图.
乐平街上新开张了一家“好又多”超市,这个星期天,张明和妈妈去这家新开张的超市买东西,如图反映了张明从家到超市的时间t(分钟)与距离s(米)之间关系的一幅图.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
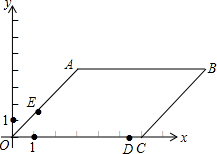 如图:在平面直角坐标系中,平行四边形OABC,O是坐标原点,OC在x轴的正半轴上,OC=6,B(9,4)
如图:在平面直角坐标系中,平行四边形OABC,O是坐标原点,OC在x轴的正半轴上,OC=6,B(9,4)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
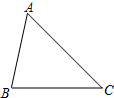 在锐角△ABC中,AB=5,BC=6,∠ACB=45°(如图),将△ABC绕点B按逆时针方向旋转得到△A′BC′(顶点A、C分别与A′、C′对应),当点C′在线段CA的延长线上时,则AC′的长度为( )
在锐角△ABC中,AB=5,BC=6,∠ACB=45°(如图),将△ABC绕点B按逆时针方向旋转得到△A′BC′(顶点A、C分别与A′、C′对应),当点C′在线段CA的延长线上时,则AC′的长度为( )| A. | $\sqrt{2}$+$\sqrt{7}$ | B. | 3$\sqrt{2}$-$\sqrt{7}$ | C. | 3$\sqrt{2}$+$\sqrt{7}$ | D. | 3-$\sqrt{7}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com