
【题目】如图,点![]() 是
是![]() 的内心,
的内心,![]() 的延长线和
的延长线和![]() 的外接圆圆
的外接圆圆![]() 相交于点
相交于点![]() ,过
,过![]() 作直线
作直线![]() .
.
(1)求证:![]() 是圆
是圆![]() 的切线;
的切线;
(2)若![]() ,
,![]() ,求优弧
,求优弧![]() 的长.
的长.
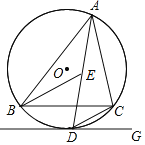
【答案】(1)见解析;(2)优弧![]() 的长=
的长=![]() .
.
【解析】
(1)连接OD交BC于H,如图,利用三角形内心的性质得到∠BAD=∠CAD,则![]() ,利用垂径定理得到OD⊥BC,BH=CH,从而得到OD⊥DG,然后根据切线的判定定理得到结论;
,利用垂径定理得到OD⊥BC,BH=CH,从而得到OD⊥DG,然后根据切线的判定定理得到结论;
(2)连接BD、OB,如图,先证明∠DEB=∠DBE得到DB=DE=6,再利用正弦定义求出∠BDH=60°,则可判断△OBD为等边三角形,所以∠BOD=60°,OB=BD=6,则∠BOC=120°,然后根据弧长公式计算优弧![]() 的长.
的长.
(1)证明:连接![]() 交
交![]() 于
于![]() ,如图,
,如图,

∵点![]() 是
是![]() 的内心,
的内心,
∴![]() 平分
平分![]() ,
,
即![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() 是圆
是圆![]() 的切线;
的切线;
(2)解:连接![]() 、
、![]() ,如图,
,如图,
∵点![]() 是
是![]() 的内心,
的内心,
∴![]() ,
,
∵![]() ,
,
∴![]()
∴![]() ,
,
∵![]() ,
,
在![]() 中,
中,![]() ,
,
∴![]() ,
,
而![]() ,
,
∴![]() 为等边三角形,
为等边三角形,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴优弧![]() 的长=
的长=![]() .
.


科目:初中数学 来源: 题型:
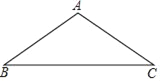
【题目】如图,在△ABC中,AB=AC=5,sinC=![]() ,将△ABC绕点A逆时针旋转得到△ADE,点B、C分别与点D、E对应,AD与边BC交于点F.如果AE∥BC,那么BF的长是____.
,将△ABC绕点A逆时针旋转得到△ADE,点B、C分别与点D、E对应,AD与边BC交于点F.如果AE∥BC,那么BF的长是____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:抛物线![]() :
:![]() (
(![]() 、
、![]() 、
、![]() 为常数,且
为常数,且![]() )与
)与![]() 轴分别交于
轴分别交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() .
.
(1)求抛物线![]() 的表达式;
的表达式;
(2)将![]() 平移后得到抛物线
平移后得到抛物线![]() ,点
,点![]() 、
、![]() 在
在![]() 上(点
上(点![]() 在点
在点![]() 的上方),若以点
的上方),若以点![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是正方形,求抛物线
为顶点的四边形是正方形,求抛物线![]() 的解析式.
的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知点P0的坐标为(2,0),将点P0绕着原点O按逆时针方向旋转60°得点P1,延长OP1到点P2,使OP2=2OP1,再将点P2绕着原点O按逆时针方向旋转60°得点P3,则点P3的坐标是_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com