
 如图,在长方形ABCD中,AB=CD=5厘米,AD=BC=4厘米.动点P从A出发,以1厘米/秒的速度沿A→B运动,到B点停止运动;同时点Q从C点出发,以2厘米/秒的速度沿C→B→A运动,到A点停止运动.设P点运动的时间为t秒(t>0),
如图,在长方形ABCD中,AB=CD=5厘米,AD=BC=4厘米.动点P从A出发,以1厘米/秒的速度沿A→B运动,到B点停止运动;同时点Q从C点出发,以2厘米/秒的速度沿C→B→A运动,到A点停止运动.设P点运动的时间为t秒(t>0),分析 (1)分别用含t的式子表示出AP、BQ,根据AP=BQ,可得t的值.
(2)分两种情况讨论,①当点Q在CB上时,②当点Q运动至BA上时,分别表示出△ADP及△BQD的面积,建立方程求解即可.
解答 解:(1)当点Q在BC边上运动时,
AP=t,BQ=4-2t,
由题意得:t=4-2t,
解得:t=$\frac{4}{3}$;
即当点Q在BC边上运动时,t为$\frac{4}{3}$时,AP=BQ;
(2)①当点Q在CB上时,
如图1所示: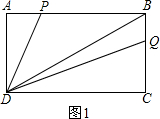
S△ADP=$\frac{1}{2}$AD×AP=2t,S△BQD=$\frac{1}{2}$BQ×DC=$\frac{5}{2}$(4-2t),
则2t=$\frac{5}{2}$(4-2t),
解得:t=$\frac{10}{7}$;
②当点Q运动至BA上时,
如图2所示:
S△ADP=$\frac{1}{2}$AD×AP=2t,S△BQD=$\frac{1}{2}$BQ×DA=2(2t-4),
则2t=2(2t-4),
解得:t=4;
③t=5s时,S△ADP=S△BQD;
综上可得:当t=$\frac{10}{7}$s或4s后5s时,S△ADP=S△BQD.
点评 本题考查了四边形综合题,难点在第二问,注意分类讨论,隐含的步骤为判断t的值是否符合题意,即判断此时的点Q是否在讨论的边上.


科目:初中数学 来源: 题型:填空题
 (1)如图,∠ABC与∠EAD是直线AD和直线BC被直线BE所截形成的同位角,∠ABC与∠BCD是直线AB和直线CD被直线BC所截形成的同旁内角
(1)如图,∠ABC与∠EAD是直线AD和直线BC被直线BE所截形成的同位角,∠ABC与∠BCD是直线AB和直线CD被直线BC所截形成的同旁内角查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
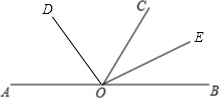 如图,A、O、B三点在同一直线上,OD是∠AOC的平分线,OE是∠BOC的平分线
如图,A、O、B三点在同一直线上,OD是∠AOC的平分线,OE是∠BOC的平分线查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 为了解某地区居民的防火意识,对该地区的初中生进行调查 | |
| B. | 为了解某商场的平均日营业额,选在周末进行调查 | |
| C. | 为了解某校1200名学生的视力情况,随机抽取该校120名学生进行调查 | |
| D. | 为了解全校学生课外小组的活动情况,对该校的男生进行调查 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com