
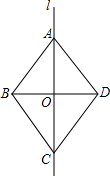
 如图,直线l是四边形ABCD的对称轴,若AD∥BC,则下列结论:(1)AB∥CD;(2)AB=AD;(3)BO=CO,(4)BD平分∠ABC.其中正确的有(1)(2)(4)(填序号).
如图,直线l是四边形ABCD的对称轴,若AD∥BC,则下列结论:(1)AB∥CD;(2)AB=AD;(3)BO=CO,(4)BD平分∠ABC.其中正确的有(1)(2)(4)(填序号). 分析 根据轴对称的性质可得∠1=∠2,∠3=∠4,根据两直线平行,内错角相等可得∠2=∠3,从而得到∠1=∠3=∠4,然后根据内错角相等,两直线平行可得AB∥CD,等角对等边可得AB=BC,再根据等腰三角形三线合一的性质可得BD平分∠ABC,AO=CO.
解答 解:如图,∵直线l是四边形ABCD的对称轴,
∴∠1=∠2,∠3=∠4,
∵AD∥BC,
∴∠2=∠3,
∴∠1=∠3=∠4,
∴AB∥CD,AB=BC,故(1)(2)正确;
由轴对称的性质,AC⊥BD,
∴BD平分∠ABC,AO=CO(等腰三角形三线合一),故(4)正确.
但不能得出BO=CO,故(3)错误;
综上所述,正确的是(1)(2)(3)(4).
故答案为:(1)(2)(4).
点评 本题考查了轴对称的性质,平行线的性质以及等腰三角形三线合一的性质,熟记各性质是解题的关键,用阿拉伯数字加弧线表示角更形象直观.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 调往甲地(单位:吨) | 调往乙地(单位:吨) | |
| A | x | 13-x |
| B | 14-x | x-1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 直线l1:y=k1x+b与直线l2:y=k2x在同一平面直角坐标系中的图象如图所示,则关于x的不等式k2x>k1x+b的解集为( )
直线l1:y=k1x+b与直线l2:y=k2x在同一平面直角坐标系中的图象如图所示,则关于x的不等式k2x>k1x+b的解集为( )| A. | x>3 | B. | x<3 | C. | x>-1 | D. | x<-1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 △ABC在平面直角坐标系中的位置如图所示,点O为坐标原点:
△ABC在平面直角坐标系中的位置如图所示,点O为坐标原点:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
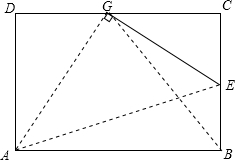 如图,矩形纸片ABCD的边AB=10cm,BC=6cm,E为BC上一点,将矩形纸片沿AE折叠,点B恰好落在CD边上的点G处,求BE的长.
如图,矩形纸片ABCD的边AB=10cm,BC=6cm,E为BC上一点,将矩形纸片沿AE折叠,点B恰好落在CD边上的点G处,求BE的长.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com