
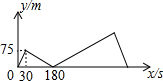
 A、B两地相距1500米,甲从A地出发慢速跑向B地,30秒后乙从A地出发快速跑向B地,乙到B地后原地休息,在跑步的整个过程中,甲、乙两人的距离y(米)与甲出发的时间x(秒)之间的关系如图所示.
A、B两地相距1500米,甲从A地出发慢速跑向B地,30秒后乙从A地出发快速跑向B地,乙到B地后原地休息,在跑步的整个过程中,甲、乙两人的距离y(米)与甲出发的时间x(秒)之间的关系如图所示.分析 (1)根据题意和图象中的数据即可求出甲、乙的速度;
(2)根据题意和函数图象可以求得各段对应的函数解析式;
(3)根据题意可以得到相应的不等式组,从而可以解答本题.
解答 解:(1)根据题意得,
甲的速度为:75÷30=2.5米/秒,
设乙的速度为m米/秒,则(m-2.5)×(180-30)=75,
解得,m=3,
则乙的速度为3米/秒;
故答案为:2.5,3;
(2)由题意可得,
当30≤x≤180时,设y与x的函数关系式为y=ax+b,
$\left\{\begin{array}{l}{30a+b=75}\\{180a+b=0}\end{array}\right.$,得$\left\{\begin{array}{l}{a=-0.5}\\{b=90}\end{array}\right.$,
即当30≤x≤180时,y与x的函数关系式为y=-0.5x+90,
乙从A地到B地的时间为:1500÷3=500,
当乙到达B地时,甲乙两人的距离为:1500-2.5×530=175,
∴当180<x≤530时,设y与x函数解析式为y=cx+d,
$\left\{\begin{array}{l}{180c+d=0}\\{530c+d=175}\end{array}\right.$,得$\left\{\begin{array}{l}{c=0.5}\\{d=-90}\end{array}\right.$,
即当180<x≤530时,y与x函数解析式为y=0.5x-90,
甲从A地到B地用的时间为:1500÷2.5=600,
当530<x≤600时,设y与x的函数关系式为y=mx+n,
$\left\{\begin{array}{l}{530m+n=175}\\{600m+n=0}\end{array}\right.$,得$\left\{\begin{array}{l}{m=-2.5}\\{n=1500}\end{array}\right.$,
即当530<x≤600时,y与x的函数关系式为y=-2.5x+1500,
由上可得,y与x的函数关系式为y=$\left\{\begin{array}{l}{-0.5x+90}&{(30≤x≤180)}\\{0.5x-90}&{(180<x≤530)}\\{-2.5x+1500}&{(530<x≤600)}\end{array}\right.$;
(3)由题意可得,
$\left\{\begin{array}{l}{0.5x-90≥100}\\{-2.5x+1500≥100}\end{array}\right.$,
解得,380≤x≤560,
答:甲、乙两人之间的距离不小于100米时,x的取值范围是380≤x≤560.
点评 本题考查一次函数的应用,解答本题的关键是明确题意,求出相应的函数解析式,利用数形结合的思想和一次函数的性质解答.


 全能测控一本好卷系列答案
全能测控一本好卷系列答案科目:初中数学 来源:2016-2017学年广东省揭阳市八年级下学期第一次月考数学试卷(解析版) 题型:填空题
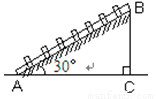
如图,修建抽水站时,沿着倾斜角为300的斜坡铺设管道,若点B离水平面的高度BC的长为30米,那么水管AB的长为_______米.
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
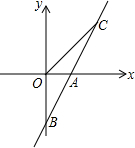 如图,直线AB与x轴交于点A(1,0),与y轴交于点B(0,-2).
如图,直线AB与x轴交于点A(1,0),与y轴交于点B(0,-2).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,已知直线y=$\frac{4}{3}$x-4与x轴、y轴分别交于A、B两点,以C(0,1)为圆心,1为半径的圆上找一动点P,连接PA、PB,则△PAB面积的最大值是( )
如图,已知直线y=$\frac{4}{3}$x-4与x轴、y轴分别交于A、B两点,以C(0,1)为圆心,1为半径的圆上找一动点P,连接PA、PB,则△PAB面积的最大值是( )| A. | 10 | B. | 9 | C. | 6+$\frac{5\sqrt{2}}{2}$ | D. | 9$\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知直线y=2x+3与直线y=-2x-1.
已知直线y=2x+3与直线y=-2x-1.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
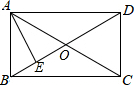 如图,矩形ABCD的对角线交于点O,∠AOB=36°,AE平分∠BAC交BD于点E,若AC=4,则AB的长度为( )
如图,矩形ABCD的对角线交于点O,∠AOB=36°,AE平分∠BAC交BD于点E,若AC=4,则AB的长度为( )| A. | $\sqrt{5}$-2 | B. | 5-$\sqrt{5}$ | C. | $\sqrt{5}$-1 | D. | 4-$\sqrt{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,四边形ABCD的面积为1,顺次连结ABCD各边中点得到四边形A1B1C1D1,再顺次连结各边中点得到四边形A2B2C2D2;重复同样的方法直到得到四边形AnBnCnDn,则四边形AnBnCnDn的面积为$\frac{1}{{2}^{n}}$.
如图,四边形ABCD的面积为1,顺次连结ABCD各边中点得到四边形A1B1C1D1,再顺次连结各边中点得到四边形A2B2C2D2;重复同样的方法直到得到四边形AnBnCnDn,则四边形AnBnCnDn的面积为$\frac{1}{{2}^{n}}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com