
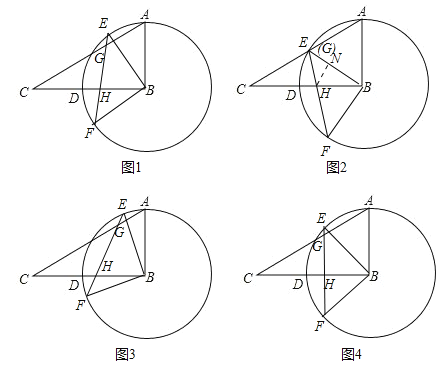
【题目】在直角三角形ABC中,∠ABC=90°,∠C=30°,AB=4,以B为圆心,BA为半径作⊙B交BC于点D,旋转∠ABD交⊙B于点E、F,连接EF交AC、BC边于点G、H.
(1)若BE⊥AC,求tan∠CGH的值;
(2)若AG=4,求△BEF与△ABC重叠部分的面积;
(3)△BHE是等腰三角形时,∠ABD逆时针旋转的度数是_____.

【答案】(1)1;(2)4![]() -4;(3)22.5°或45°.
-4;(3)22.5°或45°.
【解析】试题分析:(1)先判断出AC∥BF,进而得出∠CGH=F=45°,即可得出结论;
(2)易知当AG=4时,点G为AC中点,与点E重合,如图2,过点H作HN⊥BE于N,△BEF与△ABC重叠部分的面积就是△EBH的面积,只需运用三角函数求出HN,即可解决问题;
(3)只需将△BHE的三个内角分别作为等腰三角形的顶角进行分类讨论,就可解决问题.
试题解析:解:(1)如图1.∵BE⊥AC,BE⊥BF,∴AC∥BF,∴∠CGH=∠F=45°,∴tan∠CGH=tan45°=1;
(2)∵∠ABC=90°,∠C=30°,AB=4,∴AC=8.∵AG=4,∴点G是AC的中点,此时E与G重合,△ABE是等边三角形,如图2.过点H作于HN⊥BE于N,∠BEF=45°,BE=BF,∴∠EHN=90°﹣45°=45°=∠BEF,∴EN=HN.设HN=x,则EN=x,NB=4﹣x.在Rt△HNB中,由tan∠NBH=![]() ,得:
,得:![]() ,解得:
,解得:![]() ,∴S△EBH=
,∴S△EBH=![]() ,即△BEF与△ABC重叠部分的面积为
,即△BEF与△ABC重叠部分的面积为![]() ;
;
(3)①若∠HEB是等腰△BHE的顶角,如图3,则有∠EBH=∠EHB=![]() =67.5°,∴∠ABE=90°﹣67.5°=22.5°.
=67.5°,∴∠ABE=90°﹣67.5°=22.5°.
②若∠EHB是等腰△BHE的顶角,如图4,则有∠EBH=∠HEB=45°,∴∠ABE=90°﹣45°=45°.
③若∠EBH是等腰△BHE的顶角,则∠EBH=180°﹣45°﹣45°=90°,此时点E与点A重合,没有旋转,故舍去.
综上所述:△BHE是等腰三角形时的旋转角的度数为22.5°或45°.


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=4 cm,BC=8 cm,点P从点D出发向点A运动,运动到点A即停止;同时点Q从点B出发向点C运动,运动到点C即停止.点P,Q的速度的速度都是1 cm/s,连结PQ,AQ,CP,设点P,Q运动的时间为t(s).
(1)当t为何值时,四边形ABQP是矩形?
(2)当t为何值时,四边形AQCP是菱形?
(3)分别求出(2)中菱形AQCP的周长和面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
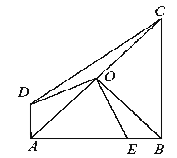
【题目】如图,四边形ABCD中,AD∥BC,∠ABC=90°,AB=BC=1,O为AC的中点,OE⊥OD交AB于点E.若AE=![]() ,则DO的长为_____________.
,则DO的长为_____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,将矩形纸片ABCD沿对角线BD向上折叠,点C落在点E处,BE交AD于点F.
(1)求证:△BDF是等腰三角形;
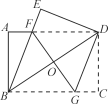
(2)如图2,过点D作DG∥BE,交BC于点G,连接FG交BD于点O.
①判断四边形BFDG的形状,并说明理由;
②若AB=6,AD=8,求FG的长.
图1
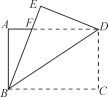
图2
查看答案和解析>>
科目:初中数学 来源: 题型:
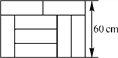
【题目】为了铺设一矩形场地,特意选择某地砖进行密铺,为了使每一部分都铺成如图所示的形状,且由8块地砖组成,问:
(1)每块地砖的长与宽分别为多少?
(2)这样的地砖与所铺成的矩形地面是否相似?试明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有这样一道题:“当a=2019,b=-3时,求多项式a2b3-![]() ab+b2-(4a2b3-
ab+b2-(4a2b3-![]() ab-b2)+(3a2b3+
ab-b2)+(3a2b3+![]() ab)-5的值”,马小虎做题时把a=2019题抄成a=-2019,但他做出的结果却是正确的,你知道这是怎么回事吗?请说明理由,并求出结果。
ab)-5的值”,马小虎做题时把a=2019题抄成a=-2019,但他做出的结果却是正确的,你知道这是怎么回事吗?请说明理由,并求出结果。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E,
(1)求证:四边形ADCE为矩形;
(2)当△ABC满足什么条件时,四边形ADCE是一个正方形?并给出证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
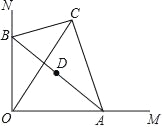
【题目】如图,在Rt△ABC中,BC=2,∠BAC=30°,斜边AB的两个端点分别在相互垂直的射线OM、ON上滑动,下列结论:
①若C、O两点关于AB对称,则OA=2![]() ;
;
②C、O两点距离的最大值为4;
③若AB平分CO,则AB⊥CO;
④斜边AB的中点D运动路径的长为![]() ;
;
其中正确的是_____(把你认为正确结论的序号都填上).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com