
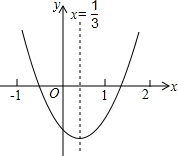
 从如图所示的二次函数y=ax2+bx+c的图象中,观察得出了下面五条信息:①c<0; ②abc>0 ③a-b+c>0 ④2a+b>0 ⑤4a+2b+c<0.你认为其中正确的信息个数有( )
从如图所示的二次函数y=ax2+bx+c的图象中,观察得出了下面五条信息:①c<0; ②abc>0 ③a-b+c>0 ④2a+b>0 ⑤4a+2b+c<0.你认为其中正确的信息个数有( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
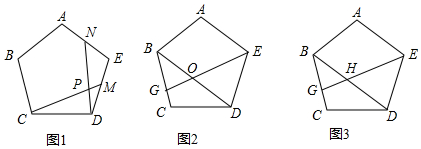
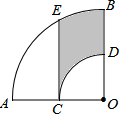 如图,在扇形AOB中,∠AOB=90°,点C为OA的中点,CE⊥OA交弧AB于点E,以点O为圆心,OC的长为半径作弧CD交OB于点D,若OA=4,则阴影部分的面积为$\frac{1}{3}$π+2$\sqrt{3}$.
如图,在扇形AOB中,∠AOB=90°,点C为OA的中点,CE⊥OA交弧AB于点E,以点O为圆心,OC的长为半径作弧CD交OB于点D,若OA=4,则阴影部分的面积为$\frac{1}{3}$π+2$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
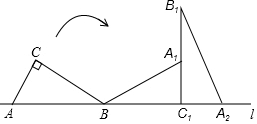 如图,Rt△ABC的斜边AB在直线l上,AC=1,AB=2.将Rt△ABC绕点B在平面内按顺时针方向旋转,使边BC落在直线l上,得到△A1BC1,再将△A1BC1绕点C1在平面内按顺时针方向旋转,使边A1C1落到直线l上,得到△A2B1C1,则点A所经过的两条弧的长度和为$\frac{13}{6}$π.
如图,Rt△ABC的斜边AB在直线l上,AC=1,AB=2.将Rt△ABC绕点B在平面内按顺时针方向旋转,使边BC落在直线l上,得到△A1BC1,再将△A1BC1绕点C1在平面内按顺时针方向旋转,使边A1C1落到直线l上,得到△A2B1C1,则点A所经过的两条弧的长度和为$\frac{13}{6}$π.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平行四边形ABCD中,过点A作AE⊥BC于点E,点F在AD上,连接CF,若∠BAE=∠FCD.
如图,在平行四边形ABCD中,过点A作AE⊥BC于点E,点F在AD上,连接CF,若∠BAE=∠FCD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
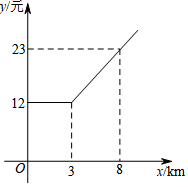 为了追求更舒适的出行体验,利用网络呼出专车的打车方式受到大众欢迎.据了解在非高峰期时,某种专车所收取的费用y(元)与行驶里程x(km)的函数关系如图所示,请根据图象解答下列问题:
为了追求更舒适的出行体验,利用网络呼出专车的打车方式受到大众欢迎.据了解在非高峰期时,某种专车所收取的费用y(元)与行驶里程x(km)的函数关系如图所示,请根据图象解答下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com