
【题目】(本题满分10分)虽然近几年无锡市政府加大了太湖水治污力度,但由于大规模、高强度的经济活动和日益增加的污染负荷,使部分太湖水域水质恶化,富营养化不断加剧。为了保护水资源,我市制定一套节水的管理措施,其中对居民生活用水收费作如下规定:
月用水量(吨) | 单价(元/吨) |
不大于10吨部分 | 1.5 |
大于10吨不大于m吨部分(20≤m≤50) | 2 |
大于m吨部分 | 3 |
(1)若某用户六月份用水量为18吨,求其应缴纳的水费;
(2)记该用户六月份用水量为x吨,缴纳水费为y元,试列出y关于x的函数关系式;
(3)若该用户六月份用水量为40吨,缴纳水费y元的取值范围为70≤y≤90,试求m的取值范围.
【答案】(1)31(元);(2)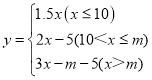 (3)25≤m≤50
(3)25≤m≤50
【解析】
试题(1)根据题意可得按照前两种收费方式收费,前面10吨每吨收1.5元,後面8吨每吨收2元,求和即可;(2)函数是分段函数,因此分表格中的三段分别求解析式;(3)用水量为40吨时就有可能是按照第二和第三两种方式收费,然后分两种情况讨论,解不等式组可得答案.
试题解析:(1)∵18<m,∴此时前面10吨每吨收1.5元,後面8吨每吨收2元
10×1.5+(18-10)×2=31(元);
(2)①当x≤10时,y=1.5x;
②当10<x≤m时,y=10×1.5+(x-10)×2=2x-5;
③当x>m时,y=10×1.5+(m-10)×2+(x-m)×3=3x-m-5;
则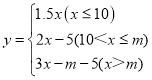
(3)∵20≤m≤50,∴当用水量为40吨时就有可能是按照第二和第三两种方式收费
①当40≤m≤50时,费用=2×40-5=75,符合题意
②当20≤m<40时,费用=3x-m-5,则:
70≤3x-m-5≤90,70≤115-m≤90,25≤m≤45,所以此状况下25≤m<40.
综合①、②,可得25≤m≤50.


 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,AB的垂直平分线MN交AC于点D,交AB于点E.

(1)求证:△ABD是等腰三角形;
(2)若∠A=40°,求∠DBC的度数;
(3)若AE=6,△CBD的周长为20,求△ABC的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,∠BAC=90°,AB=AC.MN是过点A的直线,BD⊥MN 于D,CE⊥MN于E.
(1)求证:BD=AE.
(2)若将MN绕点A旋转,使MN与BC相交于点G(如图2),其他条件不变,求证:BD=AE.
(3)在(2)的情况下,若CE的延长线过AB的中点F(如图3),连接GF,求证:∠AFE=∠BFG.
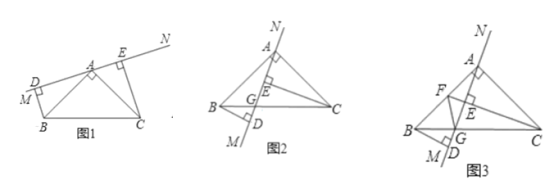
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在平面直角坐标系中,圆心为P(x,y)的动圆经过点A(1,2)且与x轴相切于点B.
(1)当x=2时,求⊙P的半径;
(2)求y关于x的函数解析式,请判断此函数图象的形状,并在图②中画出此函数的图象;
(3)请类比圆的定义(图可以看成是到定点的距离等于定长的所有点的集合),给(2)中所得函数图象进行定义:此函数图象可以看成是到 的距离等于到 的距离的所有点的集合.
(4)当⊙P的半径为1时,若⊙P与以上(2)中所得函数图象相交于点C、D,其中交点D(m,n)在点C的右侧,请利用图②,求cos∠APD的大小.
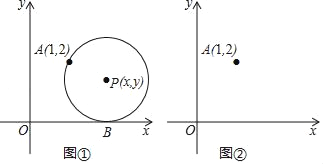
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知图1为一个正方体,其棱长为12,图2为图1的表面展开图(数字和字母写在外面),请根据要求回答问题:
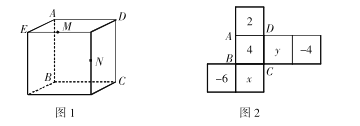
(1)若正方体相对面上的数互为相反数,则![]() _________;
_________;
(2)用一个平面去截这个正方体,下列关于截面(截出的面)的形状的结论:①可能是锐角三角形;②可能是直角三角形;③可能是钝角三角形;④可能是平行四边形.其中所有正确结论的序号是( );
A.①② B.①④ C.①②④ D.①②③④
(3)图1中,![]() 为所在棱的中点,请在图2标出点
为所在棱的中点,请在图2标出点![]() 的位置,并求出
的位置,并求出![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:线段![]() .
.
(1)如图1,点![]() 沿线段
沿线段![]() 自
自![]() 点向
点向![]() 点以
点以![]() 秒运动,同时点
秒运动,同时点![]() 沿线段
沿线段![]() 自
自![]() 点向
点向![]() 点以
点以![]() 秒运动.
秒运动.
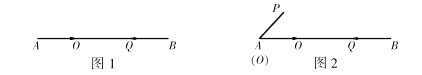
①问经过几秒后![]() 相遇?
相遇?
②几秒钟后![]() 相距
相距![]() ?
?
(2)如图2,![]() ,
,![]() ,点
,点![]() 以每秒
以每秒![]() 沿线段
沿线段![]() 自
自![]() 点向
点向![]() 点运动,同时点
点运动,同时点![]() 沿线段
沿线段![]() 自
自![]() 点向
点向![]() 点运动,点
点运动,点![]() 自
自![]() 点向
点向![]() 点运动的同时线段
点运动的同时线段![]() 以每秒
以每秒![]() 的速度绕点
的速度绕点![]() 顺时针旋转一周停止,假如
顺时针旋转一周停止,假如![]() 两点能相遇,求点
两点能相遇,求点![]() 运动的速度.
运动的速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】农贸市场拟建两间长方形储藏室,储藏室的一面靠墙(墙长30m),中间用一面墙隔开,如图所示,已知建筑材料可建墙的长度为42m,则这两间长方形储藏室的总占地面积的最大值为_______m2.
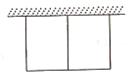
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为营造“安全出行”的良好交通氛围,实时监控道路交迸,某市交管部门在路口安装的高清摄像头如图所示,立杆MA与地面AB垂直,斜拉杆CD与AM交于点C,横杆DE∥AB,摄像头EF⊥DE于点E,AC=55米,CD=3米,EF=0.4米,∠CDE=162°。
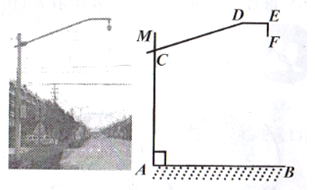
(1)求∠MCD的度数;
(2)求摄像头下端点F到地面AB的距离。(精确到百分位)
(参考数据;sin72°=0.95,cos72°≈0.31,tan72°=3.08,sin18°≈0.31,cos18°≈0.95,tan18°≈0.32)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,用棋子摆成一组“上”字:

如果按照以上规律继续摆下去,那么通过观察,可以发现:
(1)第![]() 个、第
个、第![]() 个图形中的“上”字分别需要用多少枚棋子?
个图形中的“上”字分别需要用多少枚棋子?
(2)第![]() 个图形中的“上”字需要用多少枚棋子?
个图形中的“上”字需要用多少枚棋子?
(3)七(3)班有![]() 名同学,能否让这
名同学,能否让这![]() 名同学按照以上规律恰好站成一个“上”字?若能,请计算最下面一“横”的学生数;若不能,请说明理由.
名同学按照以上规律恰好站成一个“上”字?若能,请计算最下面一“横”的学生数;若不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com