
����Ŀ��ijУ�ſ����š�ǰ��ѧУ���������С��Ľ�ָͨʾ��CD����ѧ���ۺ���ʵ����С���ͬѧ����������ָͨʾ��CD�ĸ߶ȡ���Ϊһ����������Ƕ��������²���������
��Ŀ | ���� |
���� | ������ָͨʾ��CD�ĸ߶� |
����ʾ��ͼ |
|
�������� | (1)�ӽ�ָͨʾ���µĵ�M��������ǰ��10 ����A���� (2)�ڵ�A���������Dz�á�DAM��27�㣻 (3)�ӵ�A��ֱ��MA��ǰ��10����B����(4)�ڵ�B���������Dz�á�CBA��18�㣮 |
���������С��ͬѧ�����ϱ��еIJ������ݣ������ָͨʾ��CD�ĸ߶ȣ�(�ο�����sin27���0.45��cos27���0.89��tan27���0.51��sin18���0.31��cos18���0.95��tan18���0.32)
���𰸡���ָͨʾ��CD�ĸ߶�ԼΪ1.3�ף�
��������
�ڡ�CMB�����CM�ij��ȣ��ڡ�ADM�У����DM�ij��ȣ��������CD��CM��DM�ó����.
�⣺��Rt��CMB�У�
�ߡ�CMB��90����MB��AM��AB��20�ף���CBA��18����
��CM��MB��tan 18����20tan 18��(��)��
��Rt��ADM��
�ߡ�AMD��90������MAD��27����
��DM��AM��tan 27����10tan 27��(��)��
��CD��CM��DM��20tan 18����10tan27���1.3(��)��
�𣺽�ָͨʾ��CD�ĸ߶�ԼΪ1.3�ף�


 ������ÿ�ʱ��ҵϵ�д�
������ÿ�ʱ��ҵϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�������ű�����ȫ��ͬ��ֽ��![]() ��������ֱ����ĸ���ͬ�ļ���ͼ�Σ���������ֽ�Ʊ��泯��ϴ��.
��������ֱ����ĸ���ͬ�ļ���ͼ�Σ���������ֽ�Ʊ��泯��ϴ��.

��1�������������һ�ţ�������������ͼ�������ĶԳ�ͼ�εĸ��ʣ�
��2��С����С��Լ����һ����Ϸ�������Ϊ������С���������һ��ֽ�ƣ����Żأ�����С����ʣ�µ�ֽ�����������һ�ţ�����������������ͼ�ζ�����Գ�ͼ��С����ʤ������С����ʤ�������Ϸ��ƽ�������б���������״ͼ��˵�����ɣ�ֽ����![]() ��ʾ��.
��ʾ��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
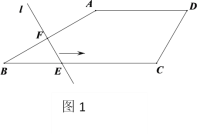
����Ŀ����ͼ1�����ı���![]() �У�
��![]() ��
��![]() ��
��![]() ,ֱ��
,ֱ��![]() .��ֱ��
.��ֱ��![]() ������
������![]() ���ӵ�
���ӵ�![]() ��ʼ����ƽ��ʱ��ֱ��
��ʼ����ƽ��ʱ��ֱ��![]() ���ı���
���ı���![]() �ı߷ֱ��ཻ�ڵ�
�ı߷ֱ��ཻ�ڵ�![]() ��
��![]() .��ֱ��
.��ֱ��![]() ����ƽ�Ƶľ���Ϊ
����ƽ�Ƶľ���Ϊ![]() ���߶�
���߶�![]() �ij�Ϊ
�ij�Ϊ![]() ����
����![]() ��
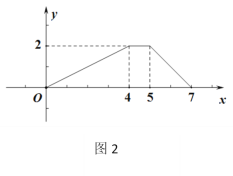
��![]() �ĺ�����ϵ��ͼ2��ʾ�����ı���
�ĺ�����ϵ��ͼ2��ʾ�����ı���![]() ���ܳ���_____.
���ܳ���_____.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() ��
��![]() ��ֱ����
��ֱ����![]() ���ң�
���ң�![]() �ǻ�
�ǻ�![]() ���е㣬����
���е㣬����![]() ��
��![]() ��ֱ��ֱ��
��ֱ��ֱ��![]() ����Ϊ
����Ϊ![]() ����
����![]() ���ӳ����ڵ�
���ӳ����ڵ�![]() ��
��
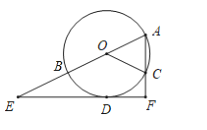
![]() ��֤:
��֤:![]() ��
��![]() �����ߣ�
�����ߣ�
![]() ��
��![]() ����
����![]() �İ뾶��
�İ뾶��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
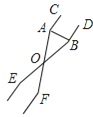
����Ŀ����ͼ��һ��ѩ��еļṹͼ����ͨ��һ���̶������һ������������������ɼ�ѩ��Ͷѩ�IJ�������������ֱ�ӽӴ�ѩ��ʹ�÷��㣬����С���ѵ�ϲ������ѩ��бպ�ʱ����á�AOB��30�㣬OA��OB��14 cm����˿�ѩ���������ѩ���ֱ��AB�ij���Ϊ________ cm��(�������һλС�����ο����ݣ�sin15���0��26��cos15���0��97��tan15���0��27)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ABCD�У�E��AB�ߵ��е㣬��EC���۾���ABCD��ʹB�����ڵ�P�����ۺ�ΪEC������AP���ӳ�AP��CD��F�㣬
��1����֤����CBE�ա�CPE��
��2����֤���ı���AECFΪƽ���ı��Σ�
��3��������ABCD�ı�AB��6��BC��4�����CPF�������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
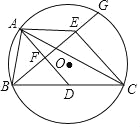
����Ŀ����ͼ����ABC�ڽ��ڡ�O��AD�ǡ�ABC�����ߣ�AE��BC������BE��AD�ڵ�F������O�ڵ�G����F��BE���е㣬����CE��
��1����֤���ı���ADCEΪƽ���ı��Σ�
��2����BC=2AB����֤: ![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������Ϊ6�������е��������ܳ�Ϊ6��������˵������ȷ���ǣ�������
A.������һ���ڱߵij����㷴����������ϵ
B.������һ���ڱߵij�������3+![]() ��3��
��3��![]()
C.������ܳ���������8
D.�������������3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У�ֱ��y��x+4��������y����![]() x2+bx+c��b��c�dz���������A��B���㣬��A��x���ϣ���B��y���ϣ�����������x�����һ������Ϊ��C��
x2+bx+c��b��c�dz���������A��B���㣬��A��x���ϣ���B��y���ϣ�����������x�����һ������Ϊ��C��

��1����������ߵĽ���ʽ��
��2��P����������һ���㣨�����A��B�غϣ���
����ͼ2������P��ֱ��AB�Ϸ�������OP��AB�ڵ�D����![]() �����ֵ��
�����ֵ��
����ͼ3������P��x����Ϸ�������PC����PCΪ����������CPEF�����ŵ�P���˶��������εĴ�С��λ��Ҳ��֮�ı䣮������E��Fǡ������y���ϣ�ֱ��д����Ӧ�ĵ�P�����꣮
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com